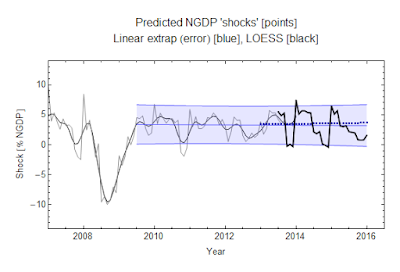
Arthur Yip on Twitter asked Noah Smith about the "101isms" in this article from a few years ago about by Michael Lind. The first myth is kind of a distillation of what many people think about economics as a science -- i.e. that it's not.
Myth 1: Economics is a science.
The way economists maintain stature in public policy circles is to present their discipline as a science, akin to physics. In Econ 101, there is no uncertainty, only the obvious truths embedded in supply and demand curves. As noted economist Lionel Robbins wrote, “Economics is the science which studies human behavior as a relationship between given ends and scarce means, which have alternative uses.” If economics is actually a science, then policy makers can feel more comfortable following the advice of economists. But if economics were really a science – which implies only one answer to a particular question — why do 40 percent of surveyed economists agree that raising the minimum wage would make it harder for people to get jobs while 40 percent disagree? It’s because as Larry Lindsey, former head of President Bush’s National Economic Council, admitted, “The continuing argument [among economists] is a product of philosophical disagreements about human nature and the role of government and cannot be fully resolved by economists no matter how sound their data.”
Science means "only one answer to a particular question"? I wrote a piece a couple weeks ago taking Daniel Little to task for this erroneous view of what science is -- I called it "Wikipedia science". It views science as a finished product. The answers to the questions all exist. One answer only. I think most people's view of falsification is similarly flawed -- even Popper thought that Einstein's equations supplanted Newtonian physics, which is news to this physicist. More accurately, Newtonian physics is an approximation to Einstein's equations for the kind of scenarios humans in the 1600s found themselves: speeds less than that of light and low gravitational field strength.
It makes sense to me that 40% agree that raising the minimum wage makes it harder for people to get jobs and 40% disagree (leaving 20% in the ¯\_(ツ)_/¯ category, I guess). If you ask physicists about dark energy, you might get similar confusion since we don't know (as a group) the answer. There are probably some physicists who think they know the specific answer, but as a field the collective answer is ¯\_(ツ)_/¯.
Science is a process, not a destination. And it's messy. I think of it more as the blind groping for which economists use the term tâtonnement. And in the history of science, you can see how the theories build on each other -- new theories tend to appear with better capacities to measure as much as new insights into nature. Quantum mechanics happens around the time we could measure the effects of quantum mechanics! These times are are loose -- quantum physics effects started to be measured in the late 1800s and the theory doesn't arrive until the 1920s or 30s.
I think that is a better way to define what is an isn't a science -- do theories change when newer and better measurements happen? And it works the other way: string theory's status as a science is likely being questioned today because we haven't made a comparable advance in measurement (a lot of the accelerator technology is comparable to where it was in the 1950s, just bigger and more efficient).
In that respect, economics is a science. There was a major measurement advance that started in the late 19th and early 20th century -- our modern concepts of GDP come from that era. Big ideas in modern economic theory date to those times. I think we are currently in the midst of another advance in measurement with "big data" as well as with the widespread availability of macro data in economics (from databases like FRED).
Maybe questioning economics as a science is like questioning string theory as a science: it has been awhile since the last empirical advance. Economics has been sitting around with the same macro data since the 1930s.
...
PS The figure caption at the article is a bit strange:
... relying on neoclassical economics, as popularized by Ludwig von Mises (left), is like a physicist today relying on Newton.
This is a bit ironic given that von Mises was against using math for economics.