The latest number came in with the highest growth rate in the past 2 years. Here it is from the perspective of the NGDP-M0 path -- where it looks like mean reversion:
A working paper exploring the idea that information equilibrium is a general principle for understanding economics. [Here] is an overview.
Saturday, October 29, 2016
3D visualizations of the interest rate model
The IT interest rate model results in the formula
log r = a log N – a log M – b
where N in nominal output (NGDP), M is the monetary base minus reserves, and a ~ 2.8 and b ~ 11.1 (pictured above). This formula represents a plane in {log N, log M, log r} space. If we wrote it in terms of {x, y, z}, we'd have
z = a x – a y – b
And we can see that the data points fall on that plane if we plot it in 3D (z being log r, while x and y are log N and log M):
Update + 4 hours
I thought it might be interesting to "de-noise" the interest rate in a manner analogous to Takens' theorem (see my post here). The basic idea is that the plane above is the low-dimensional subspace to which the data should be constrained. This means that deviations normal to that plane can be subtracted as "noise":
The constrained data is blue, the actual data is green. This results in the time series (same color scheme):
The data is typically within 16 basis points (two standard deviations or 95%) of the de-noised data.
Friday, October 28, 2016
Economist shouldn't be used as source for what is "scientific"
Update 30 October 2016: George H. Blackford responds in comments below (and here). I agree with his point that the lack of consensus on dark energy in physics is trivial (i.e. it has no effect on humans) compared with the real world consequences of a lack of consensus on economic policy. Additionally, a distinction should be drawn between Milton Friedman's "as if" methodology itself and how it is perceived in economics (e.g. Noah Smith seems to exhibit the perception, disagreeing with it [I responded to this here]). I will follow up with more after taking some time to digest George's comments.
Update 1 November 2016: We have blogging sign! The response has posted....
Ugh.
1/ Economist writing this should probably learn about science before talking about it. "As if" = "effective theory".https://t.co/xIv0antibu https://t.co/Bk78JlQXCA— Jason Smith (@infotranecon) October 28, 2016
Here we go again (here, here). The author of this terrible article is George Blackford, who has a Phd in economics. Since economics is oh so scientific in its approach, we should of course consult an economist on how to be scientific. Blackford takes a dim view of Friedman's "as if" approach:
Economists Should Stop Defending Milton Friedman’s Pseudo-science
On the pseudo-scientific nature of Friedman’s “as if” methodology
... Friedman poses [the billiard player] analogy in the midst of a convoluted argument by which he attempts to show that a scientific theory (hypothesis or formula) cannot be tested by testing the realism of its assumptions. All that matters is the accuracy of a theory’s predictions, not whether or not its assumptions are true.
Let me borrow from Wikipedia:
Effective theory
In science, an effective theory is a scientific theory which proposes to describe a certain set of observations, but explicitly without the claim or implication that the mechanism employed in the theory has a direct counterpart in the actual causes of the observed phenomena to which the theory is fitted. I.e. the theory proposes to model a certain effect, without proposing to adequately model any of the causes which contribute to the effect. ...
In a certain sense, quantum field theory, and any other currently known physical theory, could be described as "effective", as in being the "low energy limit" of an as-yet unknown "Theory of Everything".
The extra underlining is mine. The way physicists understand all of physics today is as an effective theory. Planets move according to Einstein's general relativity as if spacetime was a kind of 4-dimensional rubber sheet bent by energy. In fact, gravity might well be a fictitious entropic force based on information at the horizon. Or it could be strings. But for most purposes, it behaves as if it is a rubber sheet.
So what Blackford considers to be pseudo-science is in fact precisely science. That's a pretty bad starting point, but it keeps getting funnier every time I read it ...
Now it seemed quite clear to me back in 1967, and it still seems quite clear to me today, that it is the purview of engineering, not science, to catalog the circumstances under which a theory works and does not work and to estimates the errors in the predictions of theories along with the cost involved in using one approach or another.
I busted out laughing when I read this. Funny story. One of the people on my committee at my thesis defense asked me exactly this question about the chiral quark soliton model -- where does it work, and where does it fail. Little did I know that Blackford had figured out back in 1967 that this kind of question should have been reserved for an engineering graduate student, not a theoretical physicist. I've been using Noah Smith's words for this: defining "scope conditions".
I also work as an engineer, and this is not what engineers do either. Engineers design and build systems using existing science. Sometimes they find limits or new things when they do.
Blackford continues to demonstrate his naivete about science:
The fundamental paradigm of economics that emerged from this methodology not only failed to [anticipate] the Crash of 2008 and its devastating effects, it has proved incapable of producing a consensus within the discipline as to the nature and cause of the economic stagnation we find ourselves in the midst of today.
In order to tell whether or not the global financial crisis could be anticipated by the correct economic theory, you would in fact have to have that correct economic theory in hand. As it goes, modern economics generally says the timing of recessions, like say, the timing of earthquakes, is random. Therefore the failure to anticipate the crisis is not evidence against the theory. In fact, it is actually the ability to anticipate the crisis that would be evidence against it! [However, this does not however confirm the theory. Just because you can't predict crises, doesn't mean no one can predict crises.]
Currently physicists are incapable of producing a consensus within the discipline as to the nature of dark energy. Does this mean the fundamental paradigm of physics is flawed? No, it just means you don't understand everything yet.
I called this naive view of science "wikipedia science". Everything is supposed to have a consensus answer already. This is how science that is taught in grade school works, but not how science as practiced by scientists works.
Some other funny bits ...
Newton’s second law assumes that force is equal to mass times acceleration.
It does not. It defines force as the rate of change of momentum.
If it could have been shown that any of the assumptions on which the derivation of the Newtonian understanding of this law depend were demonstrably false, the Newtonian understanding of this law would most certainly not have been accepted, at least not by physicists.
I like the idea of physicists existing at the time of Newton. Reading his journal articles and writing comments in response. But they were called natural philosophers (physic had more to do with medicine at the time), and there really wasn't a codified scientific method at the time. People had accepted hundreds of things that were demonstrably false at the time -- and "physicists" understood Galileo's bodies falling at the same rate without air resistance despite no experiment being done until hundreds of years later.
I also assume c = ∞ (or more technically v/c << 1) all the time. It is demonstrably false (for hundreds of years). Basically, I take Galilean invariance to be an effective description of Lorentz invariance. The most accurate theory in the universe (quantum field theory) assumes spacetime isn't curved (even though it is).
... all of the major advances in the physical sciences that have come about since the time of Galileo were accomplished as a result of 1) Galileo rejecting the unrealistic assumptions of Aristotle, 2) Newton rejecting the unrealistic assumptions of Galileo, and 3) Einstein rejecting the unrealistic assumptions of Newton
The assumptions weren't rejected because they were unrealistic. They were rejected because the theory was wrong and a new theory was put forward that was more empirically accurate.
I also know some biologists and chemists that would probably object to saying this about "all of the major advances in the physical sciences".
[Update 31 August 2017: I also want to say that this is also just totally false. None of Newton's assumptions were rejected by Einstein. Einstein just added an assumption that the speed of light is constant in all frames of reference. Additionally, Newton didn't reject anything Galileo wrote as far as I am aware.]
[Update 31 August 2017: I also want to say that this is also just totally false. None of Newton's assumptions were rejected by Einstein. Einstein just added an assumption that the speed of light is constant in all frames of reference. Additionally, Newton didn't reject anything Galileo wrote as far as I am aware.]
... mainstream economists justified on the basis of an economic theory that assumes speculative bubbles cannot exist ...
This is not an assumption, but a consequence of the assumptions (that agents are rational), and in fact a consequence of one particular economic theory. There is lots of research in this area. For example, here is my copy of mainstream economists Carmen Reinhart and Kenneth Rogoff's book [pdf]:
This is also pretty funny:
Friedman is quite wrong in his assertion that there is a “thin line . . . which distinguishes the ‘crackpot’ from the scientist.” That line is not thin. It is the clear, bright line that exists between those who accept arguments based on circular reasoning and false assumptions as meaningful and those who do not.
There may be a bright line, but given the things he's said, I'm not sure Blackford knows where it is. He should definitely not be the one guiding us.
...
To be continued ...
... And here we go:
Friedman argues that the relevance of a theory cannot be judged by the realism of its assumptions so long as it is also argued that it is as if its assumptions were true. Aside from the fact that this argument makes absolutely no sense at all as a foundation for scientific inquiry, it begs the question: Why should mainstream economists be taken seriously if their theories and, hence, their arguments are based on false assumptions?
Now it is true that saying a theory is an effective theory are not a defense against investigating the assumptions. "False" (according to understanding at the time) assumptions leading to a correct understanding or empirical success are a really good source of new discoveries. For example, according to all known science at the time, discrete, quantized photons were in contradiction to the enormously successful Maxwell's theory of continuous electromagnetic fields. However Planck used this "false" hypothesis (at the time) and was able to describe blackbody radiation. The logical reconciliation of Maxwell and Planck's hypothesis did not come until fifty years later with quantum electrodynamics.
Basically, there is no way to tell whether "false" assumptions we have today are really "false" in the eventual theory. Rational agents are "false" empirically based on experiments with real humans. Homo economicus is very different from Homo sapiens. However, it may well be that Homo economicus is emergent. So saying the assumption of rational agents is false might be correct for the micro theory, but is wrong for the meso- theory and macro- theory.
Also, I can't stand this new understanding of the phrase "begs the question". That's just my opinion.
Is it any wonder that this [economic] paradigm ignores the relevance of the essential role of cooperative action through democratic government
I'm pretty sure that government spending is discussed as part of mainstream economics. Let me check. Yep [pdf]. Is this supposed to be some kind of other role? Has Blackford come up with an economic theory that is more empirically accurate than mainstream economics that fits his assumption of the primacy of government (that differs from mainstream theories where government actions matter)? If he hasn't (and he hasn't) then Blackford is being seriously hypocritical. He is committing the exact same crime (assuming an unrealistic role of government for which there is no empirical evidence) he accuses Friedman of (assuming an unrealistic role of rational agents for which there is no empirical evidence).
To the casual observer it would appear that as a result of the policies supported by mainstream economists over the past fifty years ... eventually led to the Crash of 2008
Point of fact: there have been fewer recessions in the US in the past 50 years (7) than in the prior 50 years (11). The past 50 years included the so-called "Great Moderation", and the recessions of 1966-2016 were also milder than those of 1916-1966 (which included the Great Depression). Is Blackford going to use a single data point as evidence for the failure of mainstream economics? Apparently, yes. And here he is trying to lecture people about what is "scientific"!
... the fundamental paradigm of economics that has emerged from these accomplishments is incapable of providing a consensus within the discipline of economics as to the nature and cause of the economic stagnation we find ourselves in the midst of today. To make matters worse, the kind of explanation of this stagnation given above cannot even be examined within the context of this fundamental paradigm let alone understood within this context since the effects of accumulating debt or of changes in the distribution of income are assumed to be irrelevant within this paradigm.
Just because it hasn't done so yet doesn't mean it is incapable. Again, physicists have no consensus about what dark energy is. This doesn't mean physics is incapable of coming up with one.
And you can look at economic stagnation in terms of the mainstream paradigm (and even with a neoclassical slant that Blackford continues to conflate with mainstream economics). And there have been studies of accumulating debt and income distribution. It's just hard to see any real effect in the data. And again we have an example of assumptions made because Blackford thinks they should be included, but doesn't provide us with a more empirically accurate theory based on their inclusion.
There is a big difference between mainstream economics refusing to acknowledge things that are important and mainstream economics ignoring you because those so-called important things don't seem to have a measurable effect or lead to a more accurate theory.
* * *
I'd like to take a moment and say that while unrealistic assumptions are may definitely be a soft spot in a theory, so is including things in the theory because you think they are important rather than because they have been demonstrated to improve the theory.
In the 1800s, it was considered realistic to include aether -- because waves obviously have to propagate in some medium, right? The thing is, sometimes it's hard to tell which of your assumptions are aether and which are the invariance of the speed of light ahead of time. Without comparing to the empirical data, you really don't know what's realistic and what's not.
What if both H. sapiens and H. economicus in economic theories led to the same theoretical outcome? Unrealistic assumptions about photons lead to the Einstein solid which is quite close to the better Debye model (nice discussion at the link). The existence of such results renders the unrealistic assumptions charge useless on its own. We really only know if certain assumptions lead to empirically valid outcomes. If more realistic assumptions lead to better comparisons with data, then unrealistic assumptions are a problem. However, at that point you already have a better theory! The real argument shouldn't be about the assumptions of the old theory -- just show that the new theory is better.
And that is one of the major problems I see with alternative approaches to economics.
New approaches tend to criticize the old approach in some way (not exhaustive, not orthogonal):
- Stock-flow consistent approaches criticize unrealistic accounting of the details of the stocks and flows and says that mainstream economics ignores e.g. agents' desired ratio of wealth to income
- Steve Keen's nonlinear approach criticizes the linearity of e.g. DSGE models
- Post-Keynesians say the mainstream ignores Minksy on credit cycles or what Keynes really said
- Institutionalists tell us that the mainstream ignores institutions
- The information transfer framework says that mainstream economics has misunderstood the price mechanism and made the error of assuming too much about economic agents
However, each of these, except for the last one, has failed to lead to a more empirically accurate theory. Or even one that is equally accurate! There are complaints about being ignored -- and really it makes some sense when the mainstream theories aren't very empirically accurate either. However, alternative approaches to economics will continue to be ignored until they show that they are better than mainstream theory in some quantifiable way. Usually, that is through more accurate theories. Einstein was allowed to dislodge Newton because Einstein's theory made predictions that were more accurate than Newtonian physics. It wasn't because Einstein criticized how "mainstream physicists" approached mechanics with "unrealistic assumptions". Einstein's assumptions (constant speed of light, no preferred reference frame) were considered unrealistic! The results (length contraction, time dilation, energy-mass equivalence) were considered even more unrealistic!
Blackford wants us to be scientific. Let me give a positive example. I think information transfer economics is a good example of being scientific. I probably fail sometimes, but I strive to apply my training as a theoretical physicist.\
- Clearly state your assumptions
- Show how your theory connects to mainstream economic theory
- Compare your theory to the empirical data and make predictions
- Show how your theory is better than mainstream
It's not very complicated!
And there we have the second major problem I see with alternative approaches. I feel that in the same way some progressives can't bring themselves to vote for Hillary Clinton because it might taint the purity of their progressivism, heterodox economist can't seem to say how their theories connect to mainstream economics. Don't be afraid of this! It's a great way to show your theory is consistent with lots of the empirical tests in the literature.
This is part of Sean Carroll's great crackpot (alternative science) checklist.
1. Acquire basic competency in whatever field of science your discovery belongs to.
2. Understand, and make a good-faith effort to confront, the fundamental objections to your claims within established science.
3. Present your discovery in a way that is complete, transparent, and unambiguous.
Understanding the connections to existing theory is critical to #1 and #2.
And if your theory doesn't have outputs that can be compared to data -- guess what, it's philosophy, and it can safely be ignored.
Thursday, October 27, 2016
Multiple dynamic employment growth equilibria
As part of looking at understanding something John Handley showed me on Twitter (that I am still looking at), I started to look at the employment level equilibria in the same way I looked at the unemployment rate equilibrium in this series of posts.
Note there are three differences -- each word in the noun phrase ...
We are looking at people employed, rather than unemployed.
level vs rate
We are looking at the number of people employed, rather than the fraction of people unemployed.
equilibria vs equilibrium
In the most significant difference, we are looking at multiple "entropy minima" in the growth rates rather than a single growth rate (or decline in the case of unemployment).
When I started working on this, I found that no line with a single growth rate was parallel to the employment level for the entire time series. For example, a line that is parallel since the Great Recession isn't parallel for the 1980s or 1990s (see graph below). This reflects the observation that the growth rate of employment (or analogously RGDP) seems to take a hit after recessions -- falling to a lower value.
So I windowed the data and looked for the growth rate that best matched the data (I did this by partitioning the data into bins parallel to each possible growth rate, and finding the spikiest [minimum entropy] distribution in the same manner as here).
It turns out that over the period 1955 to 2016, we have roughly three different rates. These were 3.8%, 2.6%, and 1.6% with transition points roughly at 1981 and 2000. For the politically inclined, these downshifts coincide with the elections of Ronald Reagan and George W. Bush -- coincidence? The 1980s recessions were serious, so understandably could have lead to a permanent downshift in the growth rate. However, it is sometimes debated whether the early-2000s recession was really a recession at all. Anyway, here are the results:
I fit them to the sum of a pair of logistic functions. Inside of these periods -- 1955 to 1981, 1981 to 2000, and 2000 to 2016 -- we have roughly a constant growth rate. We can then look at recessions (declines in the employment level) as logistic functions relative to that constant growth rate. If we do that, we can organize the employment data into a series of constant growth rate periods punctuated by recessions:
[Update 3 Nov 2016: I fixed the previous graph. Mathematica chopped off the 1990 dip for some reason.]
I would like to stress my use of the word organize. This is one particular model-dependent understanding of the employment data. There is no reason this data couldn't be consistent with e.g. a continuously falling employment growth rate.
Parsing the macrohistory database ... for meaning
Adding to my expanding series (here, here, here) on the macrohistory database, I thought I'd discuss the possible meanings behind the principal components (pictured above) of the long and short term interest rate time series from the 1870s to the present being approximately equal to the US time series over that period. Let me begin a (probably not exhaustive) list:
Theory 1: The US has dominated the (Western) global economy since the 1870s
It is true that the US has played a large role in the (Western) global economy, but it doesn't have its commanding lead until the post-WWII period.
Theory 2: The principal component is actually a combination of the pre-WWII Europe and the post-WWII US
We'll use the UK in our example. Before WWII, the UK dominates interest rates; after, the US does. Since the UK dominates before WWII, the pre-WWII US interest rates are basically the UK rates. Since the post-WWII rates are dominated by the US, the UK's post-WWII rates are basically the US rates. Therefore either the US or UK would work as the principal component.
Theory 3: The principal component is actually just the post-WWII US
Before WWII, interest rates in the database seem to be fluctuations around a roughly constant level and the global Great Depression. Since there's nothing differentiating them, the only feature we're extracting is the rise and fall of interest rates in the post-WWII period when the US dominates the economy. The algorithm had to choose a country for the pre-WWII piece and the US works just as well as any.
Theory 4: There is a "global economy", and the principal component gives us its interest rate
This theory says that there is some underlying global signal and each nation's interest rate represents a particular measurement of it. Each nation taps into the global "pulse" in a different way, so the time series differ. However, looking at all the data you can get a glimpse of the economic heart beat. This theory could be interpreted as a generalization of theory 2 where no one economy dominates for very long.
...
These theories are all generically related by saying that the principal component PC is a linear combination of different numbers of pieces.
1: PC = A + ε
2: PC = a A + b B + ε
3: PC = a A + X + ε
4: PC = a A + b B + c C + ... + ε
In a sense, this isn't saying much. This is practically a definition of what a principal component analysis is. It organizes our thinking, though. And this allows us to make a surprising conclusion. Interest rates in a country we'll call D are explained by factors not domestic to D. Basically,
D = d PC + ε
Where PC is primarily other countries (and might even be just one). Therefore, if demographic factors are the cause of high interest rates in your model, they are demographic factors in A (using theory 1). If monetary factors are the cause, they are monetary factors in A.
Another way to put this is that the mechanism of interest rate "importation" (i.e. how the interest rate of A becomes the interest rate of D [1], and if/how the factors domestic to D have an effect) is almost more important than the mechanism for understanding the principal component interest rate. It also means that domestic factors are usually unimportant, except when you are looking at the principal component, in which case they are very important.
I can make this more clear using the IT model as an explicit model (just imagine your favorite stand-in model if you don't like it). Let's use theory 1 above (I'll leave it as an exercise to the reader how to generalize is). In country A, interest rates are given by
log(rA) = a1 log(NA/MA) + a0
However, in country D, they are given by
log(rD) = d0 (a1 log(NA/MA) + a0) + f(ND, MD, ...)
In country D, interest rates will seem to be governed by entirely different mechanisms than those in country A.
Speculation: Does this translate into economic theories in different countries? Does country A have more attempts at "scientific"/"fundamentals" -based theories (e.g. a purely monetary model), while other countries have more "social"/"relationships" -based theories? Does country A think economics is explainable while country D thinks economics is ineffable?
...
Footnotes
[1] An example of such a mechanism would be a country having lots of foreign currency denominated debt, such as Australia with US dollar-denominated debt.
Parsing the macrohistory database: more principal components
Continuing this series ([1], [2]), I did a principal component analysis of long term interest rates (in [2], it was short term interest rates) in the macrohistory database [0] and came to roughly the same conclusion: the US is the dominant component vector. Interestingly, the distant runner up is actually Finland. It seems Finland's interest rate history is unique enough to warrant its own component.
There are no IT models here because the relevant monetary data (either MZM or base money minus reserves) is not in the macrohistory database.
...
Footnotes:
[0] Òscar Jordà, Moritz Schularick, and Alan M. Taylor. 2017. “Macrofinancial History and the New Business Cycle Facts.” in NBER Macroeconomics Annual 2016, volume 31, edited by Martin Eichenbaum and Jonathan A. Parker. Chicago: University of Chicago Press.
Tuesday, October 25, 2016
Parsing the macrohistory database: principal components
In my continuing adventures in parsing the macrohistory database [0], I noticed that most of the interest rate data looks a bit like the US interest rate time series. So I did a principal component analysis (specifically a Karhunen-Loeve decomposition).
It turns out there are three basic features of world interest rates in the macrohistory database: the US, Japan, and Germany. Here are the component vectors:
You can see the first three components are really the only ones with structure -- and they match up with the US, Germany (really only the Wiemar hyperinflation), and Japan:
As a side note, the US and Japan are the countries for which the interest rate model works the best. Additionally, if you leave out Germany [1], the US and Japan describe most of the variation of the data (i.e. the German component is mostly used to describe the Weimar hyperinflation in the German data itself).
Another way to put this is that most of the variation in the interest rate data in the macrohistory database is explained by the US data. This makes some sense: the US has been the largest economy for most of the time that the interesting variation in interest rates has happened (post-WWII). Before WWII, interest rates are relatively constant across with the low rates in the Great Depression being the only major variation [2]. Since the US interest rate captures most of the variation in the interest rate data, that means the US IT model explains most of the interest rate data -- since it captures most of the US interest rate data.
Footnotes:
[0] Òscar Jordà, Moritz Schularick, and Alan M. Taylor. 2017. “Macrofinancial History and the New Business Cycle Facts.” in NBER Macroeconomics Annual 2016, volume 31, edited by Martin Eichenbaum and Jonathan A. Parker. Chicago: University of Chicago Press.
[2] Here is that analysis:
Monday, October 24, 2016
Parsing the macrohistory database: interest rates
Update 25 October 2016: check out this follow up using principal component analysis.
I was directed to this long time series macro data [1] by a reader via email, and so thought I'd try the IT interest rate model:
I was directed to this long time series macro data [1] by a reader via email, and so thought I'd try the IT interest rate model:
log(r) = a log(NGDP/MB) + b
Only a few series fit over the entire time period with one set of parameters {a, b}, but this should be expected because e.g. several European countries are now on the Euro. So I attempted to look for a natural way to break up the data using cluster analysis to find linear segments -- finding clusters associated by a given range of years, log(r) and log(NGDP/M0). Here are the clusters for the USA and DEU:
Note these are 2D representations of a 3D graph (imagine time going into the page).
I'm still looking at the fit methodology. Some of the data doesn't need to be broken up (particularly the Anglophone countries: USA, CAN, AUS, and GBR -- though I broke up USA and AUS in the graphs below). Many of the European countries do -- and the best place to break tends to be around World War II. Some preliminary results are listed below:
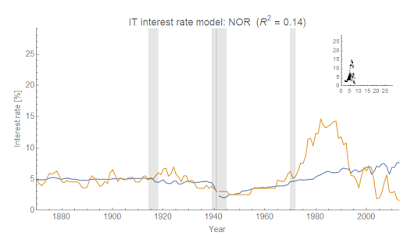
NOR and DEU (Norway and Germany) don't work very well unless you break up the data into many segments (about 4-5).
Nearly all of the countries that don't work well are currently on the Euro, or had pegged their currencies to some other currency at some point.
Anyway, this is a work in progress. I am going to try and map the break points to details of monetary history of the various countries.
...
Footnotes:
[1] Òscar Jordà, Moritz Schularick, and Alan M. Taylor. 2017. “Macrofinancial History and the New Business Cycle Facts.” in NBER Macroeconomics Annual 2016, volume 31, edited by Martin Eichenbaum and Jonathan A. Parker. Chicago: University of Chicago Press.
Saturday, October 22, 2016
Wednesday, October 19, 2016
Forecasting: IT versus all comers
On Twitter, John Handley asked about forecasting inflation with a constant 2% inflation as well as a simple AR process in response to my post about how the information transfer (IT) model holds its own against the Smets-Wouters DSGE model (see this link for the background). I responded on Twitter, but I put together a more detailed response here.
I compared the original four models (DSGE, BVAR, FOMC Greenbook, and the IT model) with four more: constant 2% (annual) inflation, an AR(1) process, and two LOESS smoothings of the data. The latter two aren't actually forecasts -- they're the actual data, just smoothed. I chose these because I wanted to see what the best possible model would achieve depending on how much "noise" you believe the data contains. I chose the smoothing parameter to be either 0.03 (achieving an R² of about 0.7, per this) or 0.54 (in order to match the R² of the IT model one quarter ahead). And here are what the four models look like forecasting one quarter ahead over the testing period (1992-2006):
So how about the performance metric (the R² of forecast vs realized inflation)? Here they are, sorted by average rank over the 1Q to 6Q horizon:
First, note that I reproduce the finding (per Noah Smith) that an AR process does better than the DSGE model. Actually, it does better than anything except what is practically data itself!
The IT model does almost exactly as well as a smoothing of the data (LOESS 0.54), which is what it is supposed to do: it is a model of the macroeconomic trend, not the fluctuations. In fact, it is only outperformed by an AR process (a pure model of the fluctuations) and a light smoothing of the data (LOESS 0.03). I was actually surprised by the almost identical performance for Q2 through Q6 of the LOESS smoothing and the IT model because I had only altered the smoothing parameter until I got (roughly) the same value as the IT model for Q1.
The DSGE model, on the other hand, is only slightly better than constant inflation, the worst model of the bunch.
Monday, October 17, 2016
What should we expect from an economic theory?
 |
| Really now ... what were you expecting? |
I got into a back and forth with Srinivas T on Twitter after my comment on an Evonomics tweet. As an aside, Noah Smith has a good piece on frequent contributor at Evonomics David Sloan Wilson (my own takes are here, here, here). I'll come back to this later. Anyway, Evonomics put up a tweet quoting an economist saying "we need to behave like scientists" and abandon neoclassical economics.
My comment was that this isn't how scientists actually behave. Newton's laws are wrong, but we don't abandon them. They remain a valid approximation when the system isn't quantum or relativistic. Srinivas took exception, saying surely I don't believe neoclassical economics is wrong in the same way Newton is wrong.
I think this gets at an important issue: what should we expect of an economic theory?
I claimed that the neoclassical approximation was good to ~10% -- showing my graph of employment. Neoclassical economics predicts 100% employment; the current value is 95%. That's a pretty good first order estimate. While Newton has much better accuracy (< 1%) at nonrelativistic speeds, this is in principle no different. But what kind of error should we expect of a social science theory? Is that 10% social science error commensurate with a < 1% "hard science" error?
I'd personally say yes, but you'd have to admit that it isn't at the "throw it out" level -- at least for a social science theory. What do you expect?
Now I imagine an argument could be made that the error isn't really 10%, but rather much, much bigger. That is hard to imagine. Supply and demand isn't completely wrong, and the neoclassical growth model (Solow) isn't completely inconsistent with the Kaldor facts. This experiment shows supply and demand functions at the micro level.
Basically, neoclassical economics hasn't really been rejected in the same way Newton is rejected for relativistic or quantum systems. Sure, there are some places where it (neoclassical economics) is wrong, but any eventual economic theory of everything is going to look just like neoclassical economics where it is right. Just like Einstein's theories reduce to Newton's for v << c (the speed of light setting the scale of the theory), the final theory of economics is going to reduce to neoclassical economics in some limit relative to some scale.
But there lies an important point, and where I sympathize with Srinivas' comment. What limit is that? Economics does not set scope conditions, so we don't know where neoclassical economics fails (like we do for Newton: v ~ c) except by trial and error.
This is where economic methodology leaves us wanting -- Paul Romer replied to a tweet of mine agreeing about this point ...
@infotranecon— Paul Romer (@paulmromer) September 24, 2016
Yes. I used to nod off when physicists interested in macro went on about scaling. I should have paid more attention.
As a theoretical physicist, I try to demonstrate by example how theoretical economics should be approached with my own information transfer framework. The ITF does in fact reduce to neoclassical economics (see my paper). But it also tells us something about scope. Neoclassical economics is at best a bound on what we should observe empirically, and holds in the market where A is traded for B as long as
I(A) ≈ I(B)
i.e. when the information entropy of the distribution of A is approximately equal to the information entropy of the distribution of B. This matches up with the neoclassical idea of no excess supply or demand (treating A as demand for B).
Now it is true that you could say I'm defending neoclassical economics because my theory matches up with it in some limit. But really causality goes the other way: I set up my theory to match up with supply and demand. Supply and demand has been shown to operate as a good first order understanding in the average case -- and even in macroeconomics the AD-AS model is a decent staring point.
Throwing neoclassical economics out is rejecting a theory because it fails to explain things that are out of scope. That is not how scientists behave. We don't throw out Newton because it fails for v ~ c.
It seems to me to be analogous to driving Keynesian economics out of macroeconomics. Keynesians did not fail to describe stagflation and e.g. the ISLM model represents a decent first order theory of macro when inflation is low. Maybe it's just that there's more appetite for criticisms of economics (per Noah Smith above):
There's a new website called Evonomics devoted to critiquing the economics discipline. ... The site appears to be attracting a ton of traffic - there's a large appetite out there for critiques of economics. ... Anyway, I like that Wilson is thinking about economics, and saying provocative, challenging things. There's really very little downside to saying provocative, challenging things, as long as you're not saying them into the ear of a credulous policymaker.
Driving out neoclassical economics seems to be politically motivated in the same way Keynesian economics was driven from macro. It's definitely not because of new data. Neoclassical economics has been just as wrong as it was in Keynes time. However, it has also been just as right.
We have to be careful about why we reject theories. We shouldn't reject 50% solutions because they aren't 100% solutions. Heck, we shouldn't reject 10% solutions because they aren't 100% solutions.
And to bring it back to my critique of David Sloan Wilson that I linked to above: we shouldn't plunge head first into completely new theories unless those theories have demonstrated themselves to be at least similarly effective as our current 50% solution. Wilson's evolutionary approach to economics hasn't even shown a single empirical success. It can't even explain why unemployment is on average between 5 and 10% in the US over the entire post-war period instead of, say, 80%. It can't explain why grocery stores work.
Neoclassical economics at least tells us that grocery stores work and unemployment is going to be closer to 0% than 100%. That's pretty good compared to anything else out there**.
** Gonna need explicit examples if you want to dispute this.
Thursday, October 13, 2016
Forecasting: IT versus DSGE
I was reading Simon Wren-Lewis's recent post, which took me to another one of his posts, which then linked to Noah Smith's May 2013 post on how poor DSGE models are at forecasting. Noah cites a paper by Edge and Gurkaynak (2011) [pdf] that gave some quantitative results comparing three different models (well, two models and a judgement call). Noah presents their conclusion:
But as Rochelle Edge and Refet Gurkaynak show in their seminal 2010 paper, even the best DSGE models have very low forecasting power.
Since this gave a relatively simple procedure (regressing forecasts with actual results), I thought I'd subject the IT model (the information equilibrium monetary model [1]) to an apples-to-apples comparison with the three models. The data is from the time period 1992 to 2006, and the models are the Smets-Wouters model (the best in class DSGE model), a Bayesian Vector Autoregression (BVAR), and the Fed "greenbook" forecast (i.e. the "judgement call" of the Fed).
Apples-to-apples is a relative term here for a couple reasons. First is the number of parameters. The DSGE model has 36 (17 of which are in the ARMA process for the stochastic inputs) and the BVAR model would have over 200 (7 variables with 4 lags). The greenbook "model" doesn't really have parameters per se (or possibly the individual forecasts from the FOMC are based on different models with different numbers of parameters). The IT model has 9, 4 of which are in the two AR(1) processes. It is vastly simpler [1].
The second reason is that the IT model's forecasting sweet spot is in the 5-15 year time frame. The IT model is about the long run trends. Edge and Gurkaynak are looking at the 1-6 quarter time frame -- i.e. the short term fluctuations.
However, despite the fact that it shouldn't hold up against these other forecasts of short run fluctuations, the scrappy IT model -- if I was to add a stochastic component to the interest rate (which I will show in a subsequent post [Ed. actually below]) -- is pretty much top dog in the average case. The DSGE model does a bit better than the IT model on RGDP growth further out, but is the worst at inflation. The Greenbook forecast does better at Q1 inflation, but that performance falls off rather quickly.
Note that even if the slope or intercept are off, a good R² indicates that the forecast could be adjusted with a linear transformation (much like many of us turn our oven to e.g. 360 °F instead of 350 °F to adjust for a constant bias of 10 °F) -- meaning the model is still useful.
Anyway, here are the table summaries of the performance for inflation, RGDP growth, and interest rates:
[Ed. this final one is updated with the one appearing at the bottom of this post.]
I also collected the R² values for stoplight charts for inflation and RGDP growth [Ed. plus the new interest rate graph from the update]:
Here is what that R² = 0.21 result looks like for RGDP growth for 1 quarter out
This is still a work in progress, but the simplest form of the IT model holds up against the best in class Smets-Wouters DSGE model. The IT model neglects the short run variation of the interest rate [Ed. update now includes] as well as the nominal shocks described by the labor supply. Anyway, I plan to update the interest rate model [Ed. added and updated] as well as do this comparison using the quantity theory of labor and capital IT model.
...
Update + 40 min
Here is that interest rate model comparison adding in an ARIMA process:
And the stoplight chart (added it above as well):
I do want to add that the FOMC Greenbook forecast is a bit unfair here -- because the FOMC sets the interest rates. They should be able to forecast the interest rate they set slightly more often than quarterly out 1Q no problem, right?
...
Update + 40 min
Here is that interest rate model comparison adding in an ARIMA process:
And the stoplight chart (added it above as well):
I do want to add that the FOMC Greenbook forecast is a bit unfair here -- because the FOMC sets the interest rates. They should be able to forecast the interest rate they set slightly more often than quarterly out 1Q no problem, right?
...
[1] The IT model I used here is
(d/dt) log NGDP = AR(1)
(d/dt) log MB = AR(1)
log r = c log NGDP/MB + b
log P = (k[NGDP, MB] - 1) log MB/m0 + log k[NGDP, MB] + log p0
k[NGDP, MB] = log(NGDP/c0)/log(MB/c0)
The parameters are c0, p0, m0, c, and b while two AR(1) processes have two parameters each for a total of nine. In a future post, I will add a third AR process to the interest rate model [Ed. added and updated].
Subscribe to:
Posts (Atom)