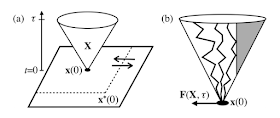
 |
| Fig. 1 from Causal entropic forces (2013). |
Recent advances in fields ranging from cosmology to computer science have hinted at a possible deep connection between intelligence and entropy maximization, but no formal physical relationship between them has yet been established. Here, we explicitly propose a first step toward such a relationship in the form of a causal generalization of entropic forces that we find can cause two defining behaviors of the human "cognitive niche" — tool use and social cooperation — to spontaneously emerge in simple physical systems. Our results suggest a potentially general thermodynamic model of adaptive behavior as a nonequilibrium process in open systems.
That's the abstract to Causal entropic forces [pdf] (2013) by Wissner-Gross and Freer (WGF) appearing Physical Review Letters. Adding causality to the description of entropic forces (entropy maximizing forces) creates systems of mindless atoms that can perform tasks that look like the actions of intelligent agents. I have previously speculated that entropy maximization can lead to emergent rational (i.e. "intelligent") economic agents and organized several posts for a future draft paper.
I suggest you read the paper, but there are a few points made in it that I'd like to emphasize. First, WGF point out entropic forces are the results of restrictions on the state space:
... an environmentally imposed excluded path-space volume ... breaks translational symmetry, resulting in a causal entropic force ... directed away from the excluded volume.
This isn't specific to 'causal' entropic forces (plain entropic forces have this same underlying reason -- something has to exclude state space volume [or more generally make it less likely] in order for you to have an entropy gradient in a specific direction). When I speculated economic forces are entropic forces dependent on the properties of the state space, that is what I had in mind. Budget constraints are constraints on the economic state space (or in e.g. Gary Becker's 1962 paper Irrational Behavior and Economic Theory, the opportunity set).
Second, WGF's causal entropic forces don't really require strict causality, just a tendency not to immediately undo a state change. The reluctance of economic agents to undo exchanges was identified by Foley and Smith as one of the differences between thermodynamics and economics. We could also potentially interpret the endowment effect as a manifestation of causal entropy.
Third, causal entropic forces acting on macroeconomic states would behave like a restorative force (rather than simply wandering around the state space if all states are equally likely). Measures like unemployment would generally return to some level determined by the state space. We'd likely find the economy near the point expected given the least informative prior, which for a high dimensional system is near the surface and in the center of the budget constraint hyperplane, not just over a long period of time, but regularly -- even after displacement from equilibrium.
This is a bit of a subtle point. If we place the economy in some state at time t where all states are equally likely, that point represents a local entropy maximum just as much as say the centroid of a high dimensional opportunity set bounded by a budget constraint hyperplane:
 |
| Budget constraint plane for consumption goods 1, 2, and 3 bounded by money M. |
However, causal entropic forces will make our state evolve towards the centroid (which is near the center of the budget constraint hyperplane of a high dimensional opportunity set) over time, instead of randomly moving through the state space (so that only on average it is near the center of the hyperplane). In a sense, this is the difference between a random walk and a random walk with drift.
Fourth, there was one aspect of List (2004) I wasn't able to reproduce with purely random transactions (entropic forces). Over time, the standard deviation of the market price fell monotonically:
As mentioned above, causal entropic forces would act like a restoring force pushing the price towards the "equilibrium" (i.e. the information equilibrium), damping deviations from it, over time.
I would also like to point out that WGF's paper is a tremendous blow to those who think humans as rational utility maximizers (or even boundedly rational, or adaptive agents) are a prerequisite for economic theory. Whatever puzzle you might think is too hard for random particles to solve, causal entropic forces are something you will have to consider.
Update 24 April 2017: In a subsequent post, I used causal entropy to simulate a demand curve:
Update 24 April 2017: In a subsequent post, I used causal entropy to simulate a demand curve:


What is the source of causal entropic force?
ReplyDeleteDoesn't the notion of a causal force entirely contradict the notion of entropy?
What is the source of causal entropic force?
DeleteMuch like an entropic force, there is no microscopic source. The force arises from entropy gradients (e.g. the "source" of the entropic force of diffusion is the non-uniform occupation of position states in the container).
Doesn't the notion of a causal force entirely contradict the notion of entropy?
Which aspect of entropy does it contradict? Entropy is a measure of the number of possible configurations of a system. Considering only causal configurations and calling that causal entropy is fine as long as you label it as such. Additionally in the long time limit the two definitions coincide (e.g. as time goes to infinity the causal volume of position states is the entire set of accessible position states).
Essentially lim t→∞ of F_t = T ∇ S_t is the entropic force formula F = T ∇ S.
Also you might consider that as the paper was published in Physical Review Letters one of the reviewers might have noticed if there was an egregious problem :)
" The force arises from entropy gradients...."
ReplyDeleteAren't these only transitory and apparent? As the system settles into entropic equilibrium will not these apparent gradients disappear?
"Considering only causal configurations and calling that causal entropy is fine as long as you label it as such."
So giving it a name renders it valid?
"Additionally in the long time limit the two definitions coincide (e.g. as time goes to infinity the causal volume of position states is the entire set of accessible position states)."
Exactly, so what's new?
Aren't these only transitory and apparent? As the system settles into entropic equilibrium will not these apparent gradients disappear?
DeleteThe entropy gradients are in configuration space, so they "always exist". The system just experiences the entropic force if it finds itself in a part of configuration space where there is a gradient (e.g. any non-uniform density distribution in the diffusion case). The system will settle into equilibrium eventually (no need to call it an 'entropic' equilibrium -- thermodynamic equilibrium is where entropy is maximized); that equilibrium is a part of configuration space with no gradient (i.e. a local maximum).
Exactly, so what's new?
The part where the causal horizon is not at infinity (t < ∞).
Not sure why you put the "exactly" there. You can't simultaneously think the definition of causal entropy is invalid and that it somehow has a valid limit. And if you understood the sentence that you quoted (a prerequisite for the "exactly"), then you wouldn't have asked the question after it because you would have known that the part that is new is where t < ∞.
Have you maybe met MERW ( https://en.wikipedia.org/wiki/Maximal_Entropy_Random_Walk )? - it also maximizes entropy, but is a bit different.
ReplyDeleteThanks for the tip -- I haven't looked at that approach before.
DeleteInterestingly the formulation looks even more like a random utility discrete choice models (which are apparently equivalent to rational inattention ... which brings us full circle back to effective MaxEnt/maximum ignorance).