Except for the price level of capital being strange (and not saying it really is the price level of capital anyway, so I used the GDP deflator), this is a run of this model for the UK. It does reasonably well (at least better than this model, which doesn't work at all), but misses out on the great recession. Maybe it was more concentrated in the financial sector in the UK? Maybe it was more non-ideal information transfer than in e.g. the US? (These two questions are related in the IE model.)
CPI : NGDP ⇄ L
X : NGDP ⇄ K
The X is an irrelevant price in the capital market. We can solve these markets for the general equilibrium (as in the paper):
CPI ≡ dNGDP/dL = (n0/l0) β (L/l0)ᵝ⁻¹(K/k0)ᵞ
The information transfer indices are empirically β = 0.4 and γ = 1.0 (compared to the US, which were β = 0.8 and γ = 0.7).
...
Update 21 January 2017
Another more recent post on this same model is here.
Update
Model errors (inflation is biased high, meaning RGDP is biased low):
...
Update 21 January 2017
Another more recent post on this same model is here.
Update
Model errors (inflation is biased high, meaning RGDP is biased low):



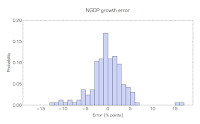


Jason, do you ever look at plot of the error (the difference between the model and the data), and do you ever see an interesting trend there? I try to eyeball it sometimes, but the noise can sometimes make the presence of a trend in the error hard to judge. It's not so bad in the above plots, but I'm thinking of previous examples.
ReplyDeleteI do plot them out, but as no one seems to be interested in these posts about the actual results of the IE model, I tend not to make it a priority.
DeleteThere are rarely trends, mostly just biases -- as illustrated above.
Thanks for the update.
DeleteI'm trying to imagine what a less data-philic version of ITE organized by taxonomy into sub-genera might sound like in a Socratic dialog:
ReplyDeleteITE School A: "The CPI : NGDP ⇄ CLF model is clearly superior due to its simplicity"
ITE School B: "But that model doesn't capture the role of capital, thus it needs augmentation!"
ITE School A: "We could try comparing it to data in different countries and see which is better."
ITE School B: "Are you kidding? The data isn't informative enough to purely reject one model over the other!"
ITE School A: "Yeah, you're right.... about that, but not about your model! Let's argue more!"
... and on and on it goes.