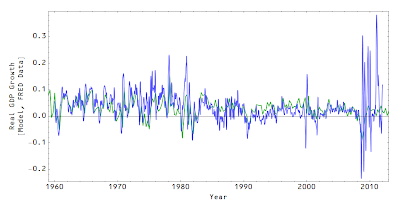
One side note from the model described in the previous post (where I assumed NGDP = monetary base growth rate + 5%, a quantity theory of money in the information transfer framework) ...
Here is a plot of the information transfer index vs annual monetary base growth rate and time (in years):
There seems to be a change in the structure of the "ideal economy" (NGDP ~ exp{(r+0.05)*t} and MB ~ exp{r*t}) at an monetary base growth rate of around r = 7% where the information transfer index starts growing (as opposed to shrinking) over time. Here are three cross sections through the previous graph at an monetary base growth rate of r = 2%, 7% and 50%:
Where this separation occurs depends on the relative normalization of the monetary base and NGDP, but it is an interesting result. High inflation economies approach an information transfer index of 1 in the long run while low inflation economies have a steady decline in the information transfer index. Note that an information transfer index of 1 is the ideal: the size of the quantity supplied (or the number of supply symbols) is equal to the demand (or the number of demand symbols).
Note that the inflation rate does not have such a separation:
(I apologize for Mathematica's placement of the contour labels.)