While I was on vacation (in Italy; Rome, Florence and Venice), I was invited (informally via email by the conference organizer, official word will come soon at which point I'll give more details) to present a paper about the information equilibrium approach this summer. Anyway, this post is going to be one of those draft paper posts that will be edited without notice.
Update: the abstract was accepted for an oral presentation. The talk will be at the 7th BioPhysical Economics meeting in DC in June 2016.
Update: the abstract was accepted for an oral presentation. The talk will be at the 7th BioPhysical Economics meeting in DC in June 2016.
Update: SLIDES!!! Allotted time is looking like 15 minutes + 5 for questions. So I might have to trim a bit.
Update: Unfortunately I had to drop out of the conference due to other obligations (i.e. my real day job).
...
Maximum entropy and information theory approaches to economics
Abstract
[Note: this has already be submitted to the conference organizers.]
In the natural sciences, complex non-linear systems composed of large numbers of smaller subunits, provide an opportunity to apply the tools of statistical mechanics and information theory. The principle of maximum entropy can usually provide shortcuts in the treatment of these complex systems. However, there is an impasse to straightforward application to social and economic systems: the lack of well-defined constraints for Lagrange multipliers. This is typically treated in economics by introducing marginal utility as a Lagrange multiplier.
Jumping off from economist Gary Becker's 1962 paper "Irrational Behavior and Economic Theory" [1] -- a maximum entropy argument in disguise -- we introduce physicists Peter Fielitz and Guenter Borchardt's concept of "information equilibrium" presented in arXiv:0905.0610v4 [physics.gen-ph] as a means of applying maximum entropy methods even in cases where well-defined constraints such as energy conservation required to define Lagrange multipliers and partition functions do not exist (i.e. economics). We show how supply and demand emerge as entropic forces maintaining information equilibrium and conditions where they fail to maintain it. This represents a step toward physicist Lee Smolin's call for a "statistical economics" analogous to statistical mechanics in arXiv:0902.4274 [q-fin.GN]. We discuss applications to the macroeconomic models presented in arXiv:1510.02435 [q-fin.EC] and non-equilibrium economics.
In 1962, University of Chicago economist Gary Becker published a paper titled "Irrational Behavior and Economic Theory". Becker's purpose was to immunize economics against attacks on the idealized rationality typically assumed in models. After briefly sparking a debate between Becker and Israel Kirzner (that seemed to end abruptly), the paper became largely forgotten.
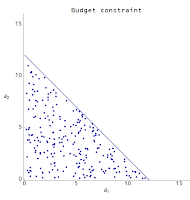
Becker's main argument was that ideal rationality was not as critical to microeconomic theory because random agents can be used to reproduce some important theorems. Consider the opportunity set (state space) given a budget constraint for two goods. An agent may select any point inside the budget constraint. In order to find which point the agents select, economists typically introduce a utility function for the agents (one good may produce more utility than the other) and then solves for the maximum utility on the opportunity set. As the price changes for one good (meaning more or less of that good can be bought given the same budget constraint), the utility maximizing point on the opportunity set moves. The effect of these price changes selects a different point on the opportunity set, tracing out a demand curve.
Instead of the agents selecting a point through utility maximization, Becker assumed every point in the opportunity set was equally likely -- that agents selected points in the opportunity set at random. In this case, the average is at the "center of mass" of the region inside the budget constraint. However, Becker showed that changing the price of one of the goods still produced a demand curve just like in the utility maximization case: microeconomics from random behavior.
There are a few key points here:- Becker is using the principle of indifference and therefore is presenting a maximum entropy argument. Without prior information, there is no reason to expect any point in the opportunity set to be more likely than any other. Each point is equally likely (equivalent points should be assigned equal probabilities). The generalization of this principle is the principle of maximum entropy: given prior information, the probability distribution that best represents the current state of knowledge is the one with maximum entropy.
- There is no real requirement that the behavior be truly random; it just must result in a maximum entropy distribution. For example, the behavior could be so complex as to appear random (e.g. chaotic), or it could be deterministic with a random distribution of initial conditions (e.g. molecules in a gas). The key requirement is that the behavior is uncoordinated -- agents do not preferentially select a specific point in the state space. Later in this presentation, we motivate the view that coordinated actions (spontaneous falls in entropy) are the mechanism for market failures (e.g. recessions, bubbles) following from human behavior (groupthink, panic, etc).
- Experiments where traditional microeconomics appears to arise spontaneously are not very surprising. From Vernon Smith's experiments using students at the University of Arizona to Keith Chen et al's [2] experiments using capuchin monkeys at Yale, most agents capable of exploring the opportunity set (state space) will manifest some microeconomic behavior.
- In the paper, Becker adds the assumption that the average must saturate the budget constraint in order to more completely reproduce the traditional microeconomic argument. However as the number of goods increases, the dimension of the opportunity set increases. For a large number of dimensions, the "center of mass" of the opportunity set approaches the budget constraint. Therefore, instead of assuming saturation one can assume a large number of goods (see figure below).
- In this scenario, an aggregate economic force like supply and demand is following from properties of the state space (opportunity set), not from properties of the individual agents. Later in this presentation, we motivate the view that when this separation between the aggregate system behavior and the individual agent behavior happens, detailed models of agents become unnecessary. The traditional highly mathematical approach to economics is really the study of the dynamics resulting from state space properties, while the study of the breakdown of the separation between aggregate and agent behavior is more behavioral economics and social science. Another way to put this is that market failures and recessions are social science (i.e. about agents), while traditional economics is really just the study of functioning markets.
[1] Becker, Gary S. Irrational Behavior and Economic Theory. Journal of Political Economy Vol. 70, No. 1 (Feb., 1962), pp. 1-13
[2] Chen, M. Keith and Lakshminarayanan, Venkat and Santos, Laurie, The Evolution of Our Preferences: Evidence from Capuchin Monkey Trading Behavior (June 2005). Cowles Foundation Discussion Paper No. 1524. Available at SSRN: http://ssrn.com/abstract=675503
Information equilibrium: maximum entropy without constraints
The maximum entropy approach typically requires the definition of constraints (such as conservation laws), and Lagrange multipliers (such as temperature) are introduced to maintain them in optimization problems (entropy maximization, energy minimization). In economics, however, few true constraints exist. Even budget constraints aren't necessarily binding when one considers economic growth, lending and the creation of money.
Economics does in fact employ Lagrange multipliers in optimization problems. Whereas temperature is the concept introduced in thermodynamics as the Lagrange multiplier, the Lagrange multiplier in economics is marginal utility (of consumption, income, etc depending on the problem). We will take a different approach.
In order to address the issue of constraints (originally for physical systems), Peter Fielitz and Guenter Borchardt [3] developed a formalism to look at how far you could take maximum entropy arguments in the absence of constraints based on information theory, deriving some simple yet general relationships between two process variables that hold under the condition of information equilibrium. We [4] later applied these results to economic systems. Let us review the basic results.
Information equilibrium posits that the information entropy of two random processes d and s (eventually for demand and supply below) are equal, i.e.
H(d) = H(s)
where we've used the symbol H for the Shannon entropy. The Shannon (information) entropy of a random event p is the expected value of the random variable's information entropy I(p)
H(p) = E[I(p)] = Σₓ pₓ I(pₓ) = - Σₓ pₓ log(pₓ)
where the sum is taken over all the states pₓ (where Σₓ pₓ = 1). Also note that p log(p) = 0 for p = 0. There's a bit of abuse of notation in writing H(p); more explicitly you could write this in terms of a random variable X with probability function P(X):
H(X) = E[I(X)] = E[- log(P(X))]
This form makes it clearer that X is just a dummy variable. The information entropy is actually a property of the distribution the symbols are drawn from P:
H(•) = E[I(•)] = E[- log(P(•))]
How does this relate to economics? In economic equilibrium, the supply (s) and demand (d) are in information equilibrium. The (spatial, temporal) probability distribution of supply is equal to the probability distribution of demand. The distribution of a large number of random events drawn from these probability distributions will approximately coincide; we can think of these as market transactions. So in economics, we say that the information entropy of the distribution P₁ of demand (d) is equal to the information entropy of the distribution P₂ of supply (s):
E[I(d)] = E[I(s)]
E[- log(P₁(d))] = E[- log(P₂(s))]
E[- log(P₁(•))] = E[- log(P₂(•))]
and call it information equilibrium (for a single transaction here). The market can be seen as a system for equalizing the distributions of supply and demand (so that everywhere there is some demand, there is some supply ... at least in an ideal market). Let's take P to be a uniform distribution (over x = 1..σ symbols) so that:
E[I(p)] = - Σₓ pₓ log(pₓ) = - Σₓ (1/σ) log(1/σ) = - (σ/σ) log(1/σ) = log σ
The information in n such events (a string of n symbols from an alphabet of size σ with uniformly distributed symbols) is just
n E[I(p)] = n log σ
Or another way using random variable form for multiple transactions with uniform distributions:
E[- log(P₁(•)P₁(•)P₁(•)P₁(•) ... )] = E[- log(P₂(•)P₂(•)P₂(•)P₂(•) ...)]
n₁ E[- log(P₁(•))] = n₂ E[- log(P₂(•))]
n₁ E[- log(1/σ₁)] = n₂ E[- log(1/σ₂)]
n₁ log(σ₁) = n₂ log(σ₂)
Let us take n₁, n₂ >> 1 and define n₁ ≡ D/dD (in an abuse of notation where dD is an infinitesimal unit of demand) and n₂ ≡ S/dS, we can write
D/dD log(σ₁) = S/dS log(σ₂)
or
(1) dD/dS = k D/S
where we call k ≡ log(σ₁)/log(σ₂) the information transfer index (which we will generally take to be empirically measured). This differential equation defines information equilibrium. Additionally, the left hand side is the exchange rate for an infinitesimal unit of demand for an infinitesimal unit of supply -- it represents an abstract price p ≡ dD/dS.
Interestingly, before continuing on to introduce utility, a less general form of equation (1) -- with k = 1 -- was written down by economist Irving Fisher in his 1892 thesis [5] and credited to the original marginalist arguments introduced by William Jevons and Alfred Marshall.
[3] Fielitz, Peter and Borchardt, Guenter. A general concept of natural information equilibrium: from the ideal gas law to the K-Trumpler effect arXiv:0905.0610 [physics.gen-ph]
[4] Smith, Jason. Information equilibrium as an economic principle. arXiv:1510.02435 [q-fin.EC]
[5] Fisher, Irving. Mathematical Investigations in the Theory of Value and Prices (1892).
Information transfer, supply and demand
One interpretation of equation (1) and information equilibrium is as a communication channel per Shannon's original paper [6] where we interpret the demand distribution as the the information source distribution (distribution of transmitted messages) and supply distribution as the information destination distribution (distribution of received messages). The diagram looks like this
If the demand is the source of information about the allocation (distribution) of goods and services, then we can assert
E[I(d)] ≥ E[I(s)]
since you cannot receive more information than is transmitted. We call the case where information is lost non-ideal information transfer. Following the previous section, our differential equation becomes a differential inequality:
(2) p ≡ dD/dS ≤ k D/S
Use of Gronwall's inequality (lemma) tells us that our information equilibrium solutions to the differential equation (1) now become bounds on the solutions in the case of non-ideal information transfer. One initial observation: the information equilibrium price (the ideal price) now becomes an upper bound on the observed price in the case of non-ideal information transfer.
So what are the solutions to the differential equation (1)? The general solution (in the case that corresponds to what economists call general equilibrium where supply and demand adjust together) is
(D/d0) = (S/s0)ᵏ
p = k (d0/s0) (S/s0)ᵏ⁻¹
where d0 and s0 are constants. If we assume that either S or D adjusts to changes faster than the other (i.e. D ≈ D0 a constant or analogously S ≈ S0) for small changes ΔD ≡ D – d0 or ΔS ≡ S – s0, conditions that correspond to what economists call partial equilibrium, we obtain supply and demand diagrams as presented in [4]
In the case of non-ideal information transfer, these supply and demand curves represent bounds on the observed price, which will fall somewhere in the gray shaded area in the figure:
[Entropic forces]
[6] Shannon, Claude E. (July 1948). A Mathematical Theory of Communication. Bell System Technical Journal 27 (3): 379–423.
Macroeconomics
AD-AS, inflation and the quantity theory of money
Since the information equilibrium approach requires large numbers of transactions, it is actually better suited to macroeconomics than microeconomics. If instead of supply and demand, we look at aggregate supply (AS) and aggregate demand (AD), asserting information equilibrium
E[I(AD)] = E[I(AS)]
and define the abstract price to be the price level P, we reproduce the basic AD-AS model of macroeconomics using supply and demand diagrams for partial equilibrium analysis. In general equilibrium we have
(AD/d0) = (AS/s0)ᵏ
P = k (d0/s0) (AS/s0)ᵏ⁻¹
Let us introduce another variable M, so that the information equilibrium equation becomes
dAD/dAS = k AD/AS
(3) (dAD/dM) (dM/dAS) = k (AD/M) (M/AS)
using the chain rule on the LHS and inserting M/M = 1 on the RHS. If we assume M is in information equilibrium with aggregate supply (such that whenever a unit of aggregate supply is used in a transaction, it is accompanied by units of M)
E[I(M)] = E[I(AS)]
such that
dM/dAS = k' M/AS
Then equation (3) becomes:
dAD/dM = (k/k') AD/M
or if k'' ≡ k/k'
dAD/dM = k'' AD/M
meaning that aggregate demand and M are also in information equilibrium
E[I(AD)] = E[I(M)]
And we have the general equilibrium solution
(AD/d0) = (M/m0)ᵏ
P = k (d0/m0) (M/m0)ᵏ⁻¹
If P is the price level and M is the money supply, this recovers the basic quantity theory of money if k = 2 since
log P ~ (k – 1) log M
Explicitly, if the growth rate of the price level (inflation rate) is π (in economists' notation, so that P ~ exp π t) and the growth rate of the money supply is μ (so that M ~ exp μ t)
log P ~ log M ⇒ π ~ μ
In general k ≠ 2, however (empirically, k ≈ 1.6 for the US and in fact appears to change slowly over time in a way that is related to a definition of economic temperature and the liquidity trap [4]). If the growth of aggregate demand is α, then in general
α ~ k μ
π ~ (k – 1) μ
If real growth (i.e. aggregate growth minus inflation) is ρ = α – π then
(π + ρ)/π = α/π = (k μ)/((k – 1) μ)
For k >> 1, we have α ≈ π and therefore ρ << α. This represents a high inflation limit where monetary policy dominates the level of output. On the other hand, if k ≈ 1, then π ≈ 0 and P ~ constant and we have a low inflation limit (where monetary expansion has no effect on output).
Okun's Law as an information equilibrium relationship
One stylized fact of macroeconomics is Okun's law. The original paper [7] presents a relationship between changes real output and changes in unemployment. We will show that there is a fairly empirically accurate form that follows from an information equilibrium relationship.
E[I(NGDP)] = E[I(HW)]
where NGDP is nominal output (also known as aggregate demand AD) and HW is total hours worked. The information equilibrium relationship gives us the equation (if the abstract price is the consumer price index CPI)
CPI = dNGDP/dHW = k NGDP/HW
rearranging, we have
HW = k NGDP/CPI
Now NGDP/CPI is real output (RGDP) and taking a logarithmic time derivative of both sides yields (for k constant)
d/dt log HW = d/dt log RGDP
which is Okun's law (falls in real output are correlated with falls in total hours worked). This works fairly well empirically (using data for the US from FRED)
[7] Okun, Arthur M. (1962). Potential GNP, its measurement and significance
Interest rates
Another application of information equilibrium is to interest rates. If the interest rate r represents a price of money M (in information equilibrium with aggregate demand NGDP), then we can say
log r ~ log NGDP/M
However there is a difference between long term interest rates R and short term interest rates r. This can be accounted for by using different monetary aggregates for M. Empirically, the monetary base MB corresponds to short rates and physical currency (sometimes called M0) corresponds to long rates:
So that
log R ~ log NGDP/M0
log r ~ log NGDP/MB
The model in [4] adds some complications, but captures the trend over a long time series (model in blue, data for three month secondary market rates from FRED in green)

















Hey, congratulations on the invitation Jason! That's great!
ReplyDeleteCheers, Tom. The abstract still has to go through the whole conference committee, though.
DeleteOK, I won't get ahead of myself. Hopefully f2b6 isn't on the committee. Lol.
Deletef2b6 makes me think of a Borg designation ...
DeleteOr Chess move ... (a bishop or queen)
I was thinking of your admirer at EJMR.
DeleteCongratulations! :)
ReplyDeleteThanks, Bill.
DeleteSee caveat above ... :)
Jason, assuming you do get formally invited and then go present your paper, what are the chances that you'll cross paths with any commonly known macro bloggers (Cochrane, Andolfatto, Glasner, Sumner, Rowe, etc)? That would be an interesting face to face meeting! It'd be great having Glasner in the audience since he had something to do with turning you on to Becker's work in the 1st place, if I recall correctly. Well, I'll try not to get ahead of myself again here... and keep my fingers crossed that the committee isn't comprised exclusively of f2b6, Sadowski and Noah Smith. (Maybe I'm wrong, but I imagine that Sumner might actually be intrigued. His attitude could be "Great: finally I might get a coherent explanation from this guy about what on Earth he's up to!"... Lol. Same goes for Rowe.).
ReplyDeleteApproximately zero since it is more an econophysics conference.
DeleteJason, I like the presentation so far! It's very clear and easy to understand (and coming from me, that's saying something!). A few suggestions:
ReplyDelete1. You might mention that the upper-right plot in your first set of plots adds indifference curves to the upper-left plot.
2. In your point #2, you state "we motivate the view that coordinated actions (spontaneous falls in entropy) are the mechanism for market failures (e.g. recessions, bubbles) following from human behavior (groupthink, panic, etc)." You might clarify that coordinated actions are *likely* to result in these negative consequences, but not guaranteed to do so (it's possible a coordinated action could improve things, isn't it?)
3. For your plot at the bottom, I'm not clear on why 3.0 coincides with the budget constraint on the x-axis? Can this be normalized to 1.0 instead? Also, those appear to be probability distributes constructed from samples, true? Why that rather than smooth analytic curves? Also, I'd add a few words saying what is happening there in a caption: what d is and n, p, x, etc. It's not too difficult to decipher (even I did it pretty quick), but the first time I took a look I sighed because that wasn't spoon fed to me and I knew I'd have to think a bit. ;D
Actually, regarding my #3, now that I think a bit more, I'm not sure I do understand it completely.
Deleted is the number of dimensions (or goods)
xi is the amount of ith good (for a particular sample pt?)
pi is the price of the ith good (for a sample pt?)
If that's true, then xi*pi is the amount spend (for the ith random sample) on good i.
If that's true, then to find the total amount spent for the ith random sample, we should sum from i to d the product xi*pi.
To find a sample distribution, we should take N sample points, do the above calculation for each, and then plot a normalized histogram.
So what does your "n" represent?
I was able to reconstruct your d=2 and d=10 curves using a brain dead Matlab script (except normalized to 1.0 on the x-axis, thus changing the y-axis values by a factor of 3):
Clearly you used a more sophisticated method to build sample prob densities, since d=10 is already looking pretty ragged for my method, and d=100 is too big (though my d=2 looks very crisp!... a straight line).
w/o doing the math, it looks like d-1 is just the order of a polynomial for the analytic curves? i.e. p(x) = 2*x for d=2, p(x) = 10*x^9 for d=10, etc (assuming x on [0,1])?
The diagram was borrowed from another post as a placeholder until I had a chance to update it and n should be d.
DeleteAnd regarding your #2 above, I could change it to "overwhelmingly likely" since were talking about scenarios akin to where all the molecules of air line up on one side of the room, but with 10^9 instead of 10^23 as a scale.
"Overwhelmingly likely" sounds good. I was thinking of a comment I saw you respond to yesterday.
DeleteJason, if you were going to name this blog today, would it be different? Would you call it "information equilibrium economics" or "maximum entropy economics" for example?
ReplyDeleteI was originally going to use "information economics" but that already means something in econ.
DeleteBut as I don't always use information equilibrium or MaxEnt (sometimes it's non-ideal information transfer), there doesn't seem to be any reason to change it.
Equilibrium and MaxEnt carry their own preconceptions as well.
How long do you anticipate they'll give you (should it happen)? Does that include time for Q&A?
ReplyDeleteNo idea. Probably 30-40 minutes plus time for questions as is typical for conferences. The paper length doesn't necessarily correlate with the talk length.
DeleteIs the notion H(X) meant to be a scalar for any random variable X? (i.e. not taking on different values for specific values of a single random variable X, but rather a scalar value for any one X defined by distribution P)?
ReplyDeleteAre d and s in H(d) and H(s) quantity demanded and quantity supplied? What's the significance of switching to the upper case with D and S later?
Also, to derive:
dD/dS = k D/S
it was necessary to assume a uniform distribution over all σ₁ demand 'symbols' and over all σ₂ supply 'symbols' (I'm not exactly sure how you define a symbol here), but then you discuss a spatial/temporal distribution which in this figure (labeled "Transmitted distribution of messages" and "Received distributions of messages" resp. [are messages = symbols?]), appear to be non-uniform. Is there some relationship between these uniform and non-uniform probability distributions?
Also, you have two derivations of demand curves with your approach (here and here). What is the relationship between these derivations?
When I ask "are messages = symbols" I'm asking can these 2D distributions just as well be labeled "Transmitted distribution of symbols" and "Received distribution of messages?" Or perhaps "Distribution symbols transmitted" and "Distribution of symbols received?" Just off hand it seems like a message might consist of a sequence of transmitted or received symbols, but is it important which is used in the labels in that figure?
DeleteHi Tom,
DeleteMessages are just strings of symbols. In our formulation, supply and demand are just messages (strings of symbols). I imagine those messages are like grid points like f6 or b2 on a Chess board (one dimension being time and the other space if you'd like). The demand is then some string like
c8d3c2d4a6a3h7d4h4a6
and the supply is some string like
g4d2d5b7c8g2d4e5a4c1
As the strings get long enough, there is a match (transaction) for every chess board location listed.
The X in H(X) is a random variable; it doesn't have a value. Specific probabilities are frequently written as P(X = x) where X is a random variable and x is a specific value. For H(X), however, the notation H(X = x) is nonsense as H is a property of the distribution of X (i.e. X itself).
It is not actually necessary to assume uniform distribution of symbols for the derivation; it just changes the definition of k such that it depends on more than one probability value ... e.g.
k = (- p1 log p1 - (1 - p1) log (1 - p1))/(- p2 log p2 - (1 - p2) log (1 - p2))
for two Bernoulli processes
The s and d are random variables, the S and D are real variables related to the n's ... n1 = D/dD.
You write:
Delete"k = (- p1 log p1 - (1 - p1) log (1 - p1))/(- p2 log p2 - (1 - p2) log (1 - p2))"
So if p1 = 0.1 and p2 = 0.9 and p1 represents the probability for demand for a widget at location 0 (as opposed to location 1), and p2 represents the probability for supply of a widget at location 0 (as opposed to location 1), then k = 1. However probability function P1 =/= probability function P2.
Now given this k (i.e. k=1) (and suppose n₁, n₂ >> 1 as well), then for there to be information equilibrium (i.e. H(d) = H(s)), it's necessary that n₁ = n₂. But is that likely given that P1 =/= P2?
I'm not sure what I'm saying/asking here: I'm just trying to make it all a bit more concrete in my brain. It somehow seems that unmet demand for widgets is going to pile up at location 1 and/or unneeded supply for widgets is going to pile up at location 0. Is that consistent with n₁ = n₂? It seems like I took a wrong turn here somewhere. You may be a person of the concrete steppes Jason, but I'm a proud member of the concrete craniums!
I probably should have just written p instead of p1 and p2. The distributions have to be the same (just not necessarily uniform, as was your original question) otherwise there is a non-zero KL divergence (information loss).
DeleteWith the choices you selected for p1 and p2, you've matched up no-demand with yes-supply and yes-demand with no-supply. These sequences do have the same amount of information (like two binary sequences determined from a coin flip where the tails are 0 for one versus the heads are 0 for the other).
"The distributions have to be the same (just not necessarily uniform, as was your original question) otherwise there is a non-zero KL divergence (information loss)"
DeleteIf they have to always be the same (for H(d) = H(s)?), then how could k ever be any other value than 1? Isn't it possible that H(d) = H(s) and k =/= 1?
If k =/= 1, then n₁ and n₂ can be such that H(d) is still equal to H(s) (i.e. for some n₁ =/= n₂).
Even if both distributions are uniform, σ₁ may not equal σ₂ (which would again require n₁ =/= n₂ if H(d) = H(s), correct?).
And if σ₁ =/= σ₂, even though the distributions are both uniform, they're not the same.
DeleteI think a better way to say it is that k accounts for a constant information loss between the distributions if they are different but k = 1 is ambiguous and could mean either the distributions are the same or that they are complements of each other with the same information. I.e. k = 1 means that each flip of two unfair coins comes up heads equally often or one comes up tails and the other heads equally often.
DeleteEssentially, your two distributions with p1=0.1 and p2=0.9 are the same distribution, just with different labels (i.e. switch heads with tails and p2 becomes 0.1).
But there is another ambiguity: same information with just more instances of symbols. For example, the strings:
Delete1111111100010001
and
FF11
contain the same information (binary, hexadecimal). We may consider that several supply widgets are required to satisfy a single demand widget (I need 5 apples to make a pie).
Ah!... so with your binary vs hex or your apples vs apple pies example, that sounds like a case (if the distributions for supply and demand are both uniform) where (if H(d) = H(s)) n₁ =/= n₂, true? In fact if supply is binary and demand hex, then n₁ = 16*n₂, and if supply is apples and demand is pies, then n₁ = 5*n₂. Is that right? Also, k =/= 1 for these cases, right?
DeleteBTW, this is great! Thanks very much!!... great examples. I guess I "fooled myself" into thinking I was comfortable with this bit before, but there were some bits I never fully grasped.
Also, you write:
"I think a better way to say it is that k accounts for a constant information loss between the distributions"
So, there can be information loss but H(d) still equal to H(s)? (i.e. still in information equilibrium?)
BTW, in your Shannon channel diagram, what corresponds to the additive noise in the economics case? Does that correspond to (overwhelming likely destructive) coordination (i.e. group think, and panics)?
In a radio/electronic communications channel, I can't think of a case where additive thermal noise could possibly improve the information content (improve the constellation): at best I can see it not disturbing anything, and that, of course, is highly unlikely.
"then n₁ = 16*n₂, and if supply is apples and demand is pies, then n₁ = 5*n₂. Is that right?" ... Hmmm, no, let me retract that one and think about it a bit more.
DeleteI guess it's not really information loss -- it's just information loss if you look at single events. But k kind of adjusts for that so in the binary/hex case above, k = 1/4 (or k = 4, the other way) and you need a sequence with 4 times as many events (or 1/4 as many) to get the same amount of information.
DeleteThe noise in Shannon's diagram would be measurement error as well as any other source of information loss (poor market design, coordination, etc).
Yes, of course: k = 4. I confused myself: 16 is the size of the hex alphabet NOT the number of binary symbols required to make one hex symbol (i.e. not n1 vs n2). So n1 = n2/4 in that case, and that I was almost correct for the apples vs pies case (I just got it turned around): n1 = n2/5 for the apples vs pies case I think.
DeleteThis latter implies k = log(sigma1)/log(sigma2) = 5, or that sigma1 = sigma2^5. So if there are two "apple symbols" (whatever those could be), then there are 32 "pie symbols."
I did a quick scan through your latest draft paper to see if you used the information entropy (H) concept (at least early on, when first introducing the ideas), but I didn't see it. I found that a helpful addition here. Would it make sense to introduce it there as well? I like seeing the H = E{I} development here.
ReplyDeleteThis:
DeleteE[I(d)] ≥ E[I(s)]
Is actually saying something different than
I(d) ≥ I(s)
which is what the draft paper said, right? And
E[I(d)] = E[I(s)]
is a weaker condition than
I(d) = I(s)
isn't it? However, looking at latest P. Fielitz and G. Borchard paper, it appears they state this without the E[] wrapped around it.
As we discuss above, it's possible to have two distributions with equal information entropy which nonetheless represent an information loss because the distributions for source and destination themselves differ in a way which guarantees a non-zero expected loss of information (i.e. there's a KL divergence).
BTW, it seems that distributions which differ by only a scale factor do not necessarily entail a loss of information (i.e. uniform over the set of binary symbols on one side of the channel and uniform over the set of hex symbols on the other side of the channel).
So how would one apply the KL-divergence formula in that case (binary on one side and hex on the other) if the channel/system itself was bundling up sets of four contiguous binary symbols (say) and replacing them with hex symbols? It seems that when presented with such a system, we may be justified in using the value of k to modify the one distribution in relation to the other prior to calculating D?
For the non-uniform Bernoulli case (above) it appears that
D(P||Q) = 0.1*log2(0.1/0.9) + 0.9*log2(0.9/0.1) = 2.5359 bits lost due to distribution mismatches?
We know that k = 1 here, so scaling one distribution relative to the other isn't going to help. Like you point out, we could redefine heads and tails on one side and fix that, but if we don't do that, then this is a lossy system.
The difference is a matter of notation. Instead of H, we use I and instead of E[...] we would use < ... >, except we leave the ensemble averages off most of the time ... and F&B explicitly show the "thermodynamic limit" where
DeleteV = < V >
which really only makes sense as an ensemble average of an operator (individual atoms have no volume [in the model], individual people have no 'demand').
In discussion with Peter F., we thought it best to leave off some of the notational clutter. I even wanted to drop the absolute value signs.
Regarding your question about the KL divergence, the idea of a distribution becomes fuzzy since one exists over a different period of time (or at a different selection rate) than the other.
The KL divergence makes the most sense when the two distributions are close to each other (P ~ Q) and the symbol rate is the same.
Actually BPSK to QAM16 represents exactly that binary to hex conversion ... in information theory, your SNR has to go up as well as your bandwidth.
"Actually BPSK to QAM16 represents exactly that binary to hex conversion ... in information theory, your SNR has to go up as well as your bandwidth."
DeleteJason, do you think this is correct? If so, then QAM16 appears to always be at least as spectrally efficient as BPSK.
It seems to match this one pretty closely.
True for a given SNR, the QAM16 symbols are more difficult to resolve (i.e., more likely to be misread), but perhaps this is offset by more bits/symbol?
QAM16 follows the Shannon limit (my comment about bandwidth,SNR) better than BPSK ... that means QAM16 is more spectrally efficient.
DeleteMaybe my last sentence seems to suggest the opposite direction in terms of channel capacity. But I was talking about what needed to be done to your BPSK signal to match up with a QAM16 without changing your bit error rate.
Yep, I just misinterpreted your sentence.
DeleteI think as it was written, it was ambiguous at best. So it's really my fault.
DeleteBTW, is this the end of your draft presentation? Are you planning on adding any more? For 30 to 40 minutes I'd think you have plenty.
ReplyDeleteNot sure yet. Going to let it sit in my head for awhile and come back to it.
DeleteHey, congratulations on the talk being accepted! I just now noticed.
ReplyDelete