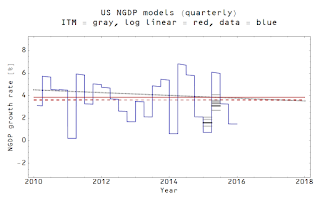
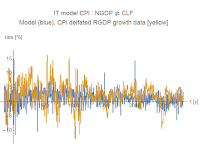
Given that I
recently put forward the idea that inflation and growth are all about labor force growth, I thought I'd clarify some things. Some of you might have asked yourself (or did ask me in comments) about how this
"new model" [1] relates to the
"old model" [2] that's all about money. I know I did.
The key thing to understand is that the information transfer framework (described in more detail
in my arXiv paper) is just that: a framework. It isn't a model itself, just a tool to build models. Those models don't have to be consistent with each other. So there really is no "new model" or "old model", just different models that may be different approximations (or one or both might become empirically invalid as more data comes in).
And as a tool, it's basically an information-theoretic realization of Marshallian supply and demand diagrams. What you do is posit an information equilibrium relationship between A and B, which I write A ⇄ B, or an information equilibrium relationship with an abstract price p = dA/dB, which I write p : A ⇄ B, and here's what's included (act now!) ...
- A general equilibrium relationship between A and B (with price p) where A and B vary together (that always applies). Generally, more A or more B leads to more B or more A, respectively.
- A partial equilibrium supply and demand relationship between A and B (with price p) with B being supply and A being demand -- it applies when either A or B is considered to move slowly with respect to the other (it's an approximation to the former where A or B is held constant).
- The possibility of "market failure" where we have non-ideal information transfer that I write A → B (all of the information from A doesn't make it to B). This leads to a non-ideal price p* < p as well as a non-ideal supply B* < B.
- A maximum entropy principle that describes what (information) equilibrium between A and B actually means, including a causality that can go in both directions along with potentially emergent entropic forces that have no formulation in terms of agents.
So in the information transfer framework there are information equilibrium relationships
A ⇄ B and more general information transfer relationships
A → B. I tend to refer to these individual relationships as "markets". Given these basic "units of model", you can construct all kinds of relationships. Traditionally crossing-diagrams are easiest. Things like
the AD-AS model or the
IS-LM model can be concisely written as the market
P : AD ⇄ AS
where AD is aggregate demand and AS is aggregate supply, or the markets
(r ⇄ p) : I ⇄ M
PY ⇄ I
PY ⇄ AS
for the IS-LM model where PY is nominal output (i.e. P × Y = NGDP, I also tend to write it N on this blog and in the paper), I is investment, M is the "money supply", p is the "price of money" and r is the interest rate.
Another aspect of the model is that information equilibrium is an equivalence relation, so that
AD ⇄ M and
M ⇄ AS implies
AD ⇄ AS (this makes
an interesting definition of money). This means that if you find a relationship (as I did in [2])
CPI : NGDP ⇄ CLF
there could be some other factor(s) X (, Y, Z, ...) such that
NGDP ⇄ X ⇄ Y ⇄ Z ⇄ CLF
Relationships like this can be inferred from a price that doesn't follow
CPI* < CPI, but can be above or below the ideal price
CPI (
CPI* < CPI or
CPI* > CPI) that follows from
being careful about the direction of information flow and the intermediate abstract prices
p₁ and
p₂ in the markets
p₁ : NGDP ⇄ X
p₂ : X ⇄ CLF
These would probably find their best analogy in "supply shocks" (price spikes due to non-ideal information transfer) as opposed to "demand shocks" (price falls due to non-ideal information transfer). Note that in the model CPI : NGDP ⇄ CLF with intermediate X, CPI = p₁ × p₂ because CPI = dNGDP/dCLF = (dNGDP/dX) (dX/dCLF) via the chain rule.
In the end, however, the only way to distinguish among different information equilibrium models (or information transfer models) is empirically. This framework works much like how quantum field theory works as a framework (as a physicist, I like to have a framework ... anything else is just philosophy). You observe something in an experiment and want to describe it. One group of researchers models it as a real scalar field and writes down a Lagrangian
ℒ = ϕ (∂² – m) ϕ
Another group models it as a spin-1/2 field
ℒ = ψ (i ∂ – m) ψ
(ok, that one's missing a slash and a bar). Both "theories" are perfectly acceptable ex ante, but ex post one or both may be incompatible with empirical data.
I was inspired to do this because of Noah Smith's recent post on why macroeconomics doesn't seem to work very well. Put simply: there is limited empirical information to choose between alternatives. My plan is to produce an economic framework that captures at least a rich subset of the phenomena in a sufficiently rigorous way that it could be used to eliminate alternatives.
I've come up with several different information equilibrium relationships -- or models built from collections of relationships (see below) -- and I am
testing their abilities with forecasts. Some might fail. Some have failed already. For example, the IS-LM model does not work if inflation is high (but represents an implicit assumption that inflation is low, so it is best to think of it as an approximation in the case of low inflation). A few of Scott Sumner's versions of his "market monetarist" model can be written as information equilibrium relationships (see below) ... and they mostly fail.
In a sense, I wanted to try to get away from the typical econoblogosphere (and sometimes even academic economics) BS where someone says "
X depends on
Y" and someone else (such as myself) would say "that doesn't work empirically in magnitude and/or direction over time" and that someone would come back with other factors
A,
B and
C that are involved at different times. I wanted a world where someone asks: is
X ⇄ Y? And then looks at the data and says yes or no. DSGE almost passes this test -- these models are at least specific enough to compare to data. However they don't ever seem to look at the data and say no ... it's always "add a financial sector" or "add behavioral economics".
There isn't enough data to support that kind of elaboration.
A good example is the quantity theory of money. It says PY = MV. Now this was great in a world where people thought V was constant (i.e. the old Cambridge k). But that turns out not to be the case and now V could depend on E[PY] or E[P] or E[M] or something else. What are these specific expectation models? Is E[P] = TIPS? Or is V ≡ PY/M is now a definition? And what is M? M2? MB?
Essentially various versions of the quantity theory of money have been falsified empirically (or at best a loose approximation when inflation is high) ... but it keeps trucking along because it doesn't exist in a framework where either its scope or validity can be challenged.
It's probably a naive hope, but it's the kind of naive hope that distinguishes "science" from "mathematical philosophy".
...
Addendum: information equilibrium models
Note that just because these models can be formulated does not mean they are correct.
I. The "quantity theory of labor" [1]
P : PY ⇄ CLF
See
this post for this one.
II. "The" IT model [2]
P : PY ⇄ M0
(r¹⁰ʸ ⇄ pᴹ⁰) : PY ⇄ M0
(r³ᵐ ⇄ pᴹᴮ) : PY ⇄ MB
P : PY ⇄ L
where the
r's represent the long and short term interest rates (3 month and 10 year),
M0 is base minus reserves, MB is the monetary base (including reserves) and
L is the labor supply (the last relationship is essentially Okun's law). I usually measure the price level
P with core PCE, but empirically it is hard to tell the difference between core PCE and core CPI (or the deflator). This model also allows the information transfer index in the first market to slowly vary. This represents a kind of
analytic continuation from a "quantity theory of money" to an "IS-LM model with liquidity trap".
III. Solow model (plus IS-LM)
PY ⇄ L
PY ⇄ K ⇄ I
K ⇄ D
1/s : PY ⇄ I
(r³ᵐ ⇄ p) : I ⇄ MB
where the last market is the IS-LM piece,
K is capital and
D is depreciation. This is a bit different from the traditional Solow model in that it is written in terms of nominal quantities. This may sound problematic, but it throws out total factor productivity as unnecessary and is
remarkably empirically accurate in describing output as well as the short term interest rate.
IV. Scott Sumner's various models (1), (2) and (3)
1)
u : NGDP ⇄ W/H
... this is just empirically wrong over more than a few years. H is total hours worked and W is total nominal wages.
2)
(W/H)/(PY/L) ⇄ u
... but H/L ⇄ u has almost no content (higher unemployment means fewer worked hours per person) and the relationship c : PY ⇄ W has a constant abstract price meaning PY = c W with c constant. The model reduces to (1/c) (H/L) ⇄ u or just the content-less H/L ⇄ u.
The correct version of both of these is P : PY ⇄ L or P : PY ⇄ H, which are just Okun's law (above).
3)
(1/P) : M/P ⇄ M
This may look a bit weird, but it could potentially work if Sumner didn't insist on an information transfer index k = 1 (if k is not 1, that opens the door to a liquidity trap, however). As it is, it predicts that the price level is constant in general equilibrium and unexpected growth shocks are deflationary in the short run.