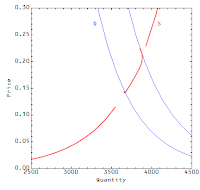
I'll start with the non-ideal information transfer picture where we assume the current price as a lower bound on how far away from ideal information transfer we are (i.e. the observed price is not the worst estimate of the ideal price).


If demand suddenly shifts lower (our constant information source drops $Q^d_0 \rightarrow Q^d_-$), the observed price will undergo a "force" to regain equilibrium, much like an ideal gas in a container where the temperature is decreased will either have the pressure or the volume (if allowed) will drop. In the case of ideal information transfer, we have restoring forces in 2 dimensions pushing the current price to the new equilibrium price. However, when there is non-deal information transfer, inside the uncertain region (shaded in red in the figures above and below) there is to first approximation no restoring force moving the price. In this figure, we show the directions of the restoring forces inside the different regions after a shift of the demand curve:

The demand curve represents the constant information source, therefore the quantity supplied (the information destination) will undergo forces acting to the left or right, depending on if the equilibrium (in the quantity dimension) is to the right or left of the demand curve. The price (the detector) will only experience a force if the equilibrium is above or below the uncertain region of the supply curve. The picture we should have is of a pressure vessel with a broken pressure gauge. If the temperature drops, the equilibrium will move to a point on the volume curve but that change may not register on the gauge.
Now assume that the price moves according to a Wiener process (random walk). If there were no forces (drift) then the price would move in a random direction and an ensemble would appear to diffuse outward from the starting point (our observed equilibrium).
If we include the forces and look at the case where there was no shift of demand, we see that the price randomly walks along the demand curve inside the uncertain region
The price versus time graph looks like a random walk
Now let us introduce a shift in the demand curve; the price then undergoes a random walk that drifts toward the new demand curve
And the price still looks like a random walk
However, if we average many such walks, we see a different price behavior
The price appears to stick near the original equilibrium
This will occur whenever the uncertain region between the demand curves is roughly symmetric along a horizontal line through the original equilibrium price or the regions above and below are sufficiently large for the top and bottom of the rough parallelogram to be considered far away from that horizontal line. What does this look like from the traditional economics perspective? You get a supply curve that flattens for downward/leftward shifts in the demand curve
Note that the price eventually drops to a price consistent with the new demand curve (it will randomly fluctuate along the new demand curve much like in the figure shown earlier).
Sticky prices are an important component of modern macroeconomics -- they are a way of saying "No, wait, demand shocks could matter as well". Keynesian and monetarist economics are based on the idea that prices don't necessarily fall to clear markets (they agree on macroeconomic stabilization policy, just not on what kind). However, these results don't completely counteract the "classical" claim, which in this framework would say that we always have ideal information transfer $I_{Q^d} = I_{Q^s}$ so that the price always falls in response to a demand shock. This seems unlikely in my own personal view.