Scott Sumner at the end of his recent post wrote a line referencing "the weakest recovery in American history". And looking at NGDP data that is a defensible statement:
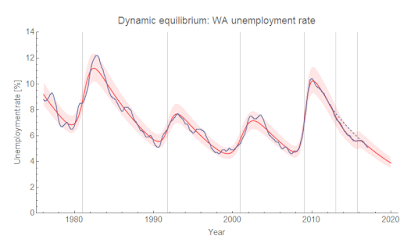
Of course, it makes little sense in terms of unemployment, which has declined at pretty much the same (fractional) rate in every recession (in fact, it declined a bit faster after 2013):
It is important to note that both of these interpretations of the data require some sort of model (I discussed this in terms of RGDP and productivity in a post from awhile ago). The former uses some kind of constant NGDP growth (RGDP growth tells a similar story) model to say that recent NGDP growth is "lower" compared to some previous average level. The latter uses the dynamic equilibrium model (and is connected to matching theory).
It turns out that we can use the dynamic equilibrium model to show that NGDP growth in the US since the recession has been "normal" and key to that understanding is that the housing bubble was not "normal" (as I've discussed before). If we give very low weighting to the data from 2004-2008, the dynamic equilibrium model is an excellent description of the post-WWII data:
The other interesting piece is that the broad trend of NGDP data since 1960 is well-described by a single shock [1] centered at 1976.6 (with width ~ 12 years) which is consistent with the single-shock description of the inflation data (a single shock centered at 1978.7 of similar width). I have hypothesized this was a demographic shock involving women entering the workforce. Using this model to frame the data trend (rather than an average as above), we have a picture of declining NGDP growth resulting from the fading of this shock ‒ a fading that had started in the 1980s. Recent NGDP growth has been consistent with an average of 3.8% [2] (the horizontal line in the figure representing the dynamic equilibrium in the absence of shocks). In this picture, the housing bubble (gray) represents a deviation from the trend (and potentially a reason why the Great Recession was so big).
It is important to point out however that this is just another model being used to frame data. One thing this model has going for it is that there's not a lot of room for policy (fiscal or monetary) choices to have had an impact on the aftermath of the Great Recession. Certainly policy choices were involved in women entering the work force (e.g. Title VII of the Civil Rights Act of 1964) and the housing bubble (e.g. deregulation). However other than those, the recovery from the Great Recession in terms of NGDP has been as it should have been expected: no tight monetary policy, no fiscal stimulus or contraction. This does not mean various policies did not have an effect on e.g. unemployment.
Just to reiterate the important point: you need a model to frame the data. Some people use average growth rates (i.e. log-linear growth). Some people eyeball the data and make an assessment (in a sense, that's what I did here regarding the housing bubble [3], although I eyeballed a particular transformation of the data [4]). But know that the model you use to frame the data can have a strong impact on your interpretation of the data.
PS Here are the results zoomed in to more recent times:
As well as the deviation from trend growth:
...
Footnotes:
[1] There is a second shock centered at 1950.9 associated with the Korean War.
[2] Coupled with core PCE inflation equilibrium of 1.7%, real growth should be about 2.1% in equilibrium (which is roughly the growth of the labor force).
[3] I did look at a version where the housing bubble represents two smaller shocks (a positive and negative one). It basically does what you'd expect: fits the red line to the housing bubble. Not very illuminating, however.
[4] That frame is this one:
Another possible frame is this one (which does make the post-recession recovery look like below-trend growth):
The difference between the two frames? The first represents equilibrium NGDP growth = 3.8%, the second NGDP growth = 5.6%. Note that this is the log of the inverse of the NGDP data with the trend growth rate subtracted. I think it helps get rid of some optical illusions caused by growth. Think of it as looking at the moon upside down from between your legs when it is at the horizon (which helps mitigate "moon illusion").