I made a forecast of PCE inflation using the dynamic information equilibrium model described in this post at the beginning of the year, and so far the model is doing well — new monthly core PCE data came out this morning:
A working paper exploring the idea that information equilibrium is a general principle for understanding economics. [Here] is an overview.
Friday, September 29, 2017
Thursday, September 28, 2017
A forecast validation bonanza
New NGDP numbers are out today for the US, so that means I have to check several forecasts for accuracy. I would like to lead with a model that I seem to have forgotten to update all year: dynamic equilibrium for the ratio of nominal output to total employed (i.e. nominal output per employed, as I write N/L):
This one is particularly good because the forecast was made near what the model saw as a turnaround point in N/L (similar to the case of Bitcoin below, also forecast near a turnaround point) saying we should expect a return towards the trend growth rate of N/L of 3.8% per annum. This return appears to be on track.
The forecast of NGDP using the information equilibrium (IE) monetary model (i.e. a single factor of production where money — in this case physical currency — is that factor of production) is also "on track":
The interesting part of this forecast is that the log-linear models are basically rejected.
In addition to NGDP, quarterly [core] PCE inflation was updated today. The NY Fed DSGE model forecast (as well as FOMC forecast) was for this data, and it's starting to do worse compared to the IE monetary model (now updated with monthly core PCE number as well):
* * *
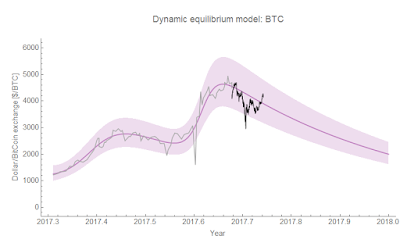
I've also checked my forecast for the Bitcoin exchange rate using the dynamic equilibrium model (which needs to be checked often because of how fast it evolves — it's time scale is -2.6/y so it should fall by about 1/2 over a quarter). It is also going well:
Tuesday, September 26, 2017
Different unemployment rates do not contain different information
I saw this tweet today, and it just kind of frustrated me as a researcher. Why do we need yet another measure of unemployment? These measures all capture exactly the same information.
I mentioned this before, however I thought I'd be much more thorough this time. I used the dynamic equilibrium model on the U3 (i.e. "headline"), U4, U5, and U6 unemployment rates and looked a the parameters.
Here are the model fits along with an indicator of where the different centers of the shocks appear as well as a set of lines showing the different dynamic equilibrium slopes (which are -0.085/y, -0.084/y, -0.082/y, and -0.078/y, respectively):
Within the error of estimating these parameters, they are all the same. How about shock magnitudes? Again, within the error of estimating the shock magnitude parameters, they are all the same:
Basically, you need one model of one rate plus 3 scale factors to describe the data. There appears to be no additional information in the U4, U5, or U6 rates. Actually in information theory this is explicit. Let's call the U3 rate random variable U3 (and likewise for the others). Now U6 = f(U3), therefore:
H(U6) ≤ H(U3)
...
Update 13 October 2017
The St. Louis Fed just put out a tweet that contains another alternative unemployment measure. It also does not contain any additional information:
Monday, September 25, 2017
Was the Phillips curve due to women entering the workforce?
Janet Yellen in her Fed briefing from last week said "Our understanding of the forces driving inflation is imperfect." At least one aspect that's proven particularly puzzling is the relationship between inflation and unemployment: the Phillips curve. In an IMF working paper from November of 2015, Blanchard, Cerutti, and Summers show the gradual fall in the slope of the Phillips curve from the 1960s to the present. I discussed it in January of 2016 in a post here. A figure is reproduced below:
Since that time, I've been investigating the dynamic equilibrium model and one thing that I noticed is that there appears to be a Phillips curve-like anti-correlation signal if you look at PCE inflation data and unemployment data:
See here for more about that graph. It was also consistent with a "fading" Phillips curve. While I was thinking about the unemployment model today, I realized that the Phillips curve might be directly connected with women entering the workforce and the impact it had on inflation via the employment population ratio. I put the fading Phillips curve on the dynamic equilibrium view of the employment population ratio for women:
We see the stronger Phillips curve signal in the second graph above (now marked with asterisks in this graph) follows the "non-equilibrium" shock of women entering the workforce. After that non-equilibrium shock fades, the employment population ratio for women starts to become highly correlated with the ratio for men — showing almost identical recession shocks.
This suggests that the Phillips curve is not just due to inflation resulting from increasing employment, but rather inflation resulting from new people entering the labor force. The Phillips curve disappears when we reach an employment-population ratio equilibrium. This would explain falling inflation since the 1990s as the employment-population ratio has been stable or falling.
Now I don't necessarily want to say the mechanism is the old "wage-price spiral" — or at least the old version of it. What if the reason is sexism? Let me explain.
A recent study showed that men self-cite more often that women in academic journals, but the interesting aspect for me was that this appears to increase right around the time of women entering the workforce:
What if the wage-price spirals of the strong Phillips curve era were due to men trying (and succeeding) to negotiate even higher salaries than women (who were now more frequently in similar jobs)? As the labor market tightens during the recovery from a recession, managers who gave a woman in the office a raise might then turn around and give a man an even larger raise. The effect of women in the workforce would be to amplify what might be an otherwise undetectable Phillips curve effect into a strong signal in the 1960s, 70s and 80s. While sexism hasn't gone away, this effect may be attenuated today from its height in that period. This "business cycle" component of inflation happens on top of an overall surge in inflation due to an increasing employment population ratio (see also Steve Randy Waldman on the demographic explanation of 1970s inflation).
Whether sexism is really the explanation, the connection betweem women entering the workforce and the Phillips curve is intriguing. It would also mean that the fading of the Phillips curve might be a more permanent feature of the economy until some other demographic phenomenon occurs.
Friday, September 22, 2017
Mutual information and information equilibrium
Natalie Wolchover has a nice article on the information bottleneck and how it might relate to why deep learning works. Originally described in this 2000 paper by Tishby et al, the information bottleneck was a new variational principle that optimized a functional of mutual information as a Lagrange multiplier problem (I'll use their notation):
\mathcal{L}[p(\tilde{x} | x)] = I(\tilde{X} ; X) - \beta I(\tilde{X} ; Y)
$$
The interpretation is that we pass the information the random variable $X$ has about $Y$ (i.e. the mutual information $I(X ; Y)$) through the "bottleneck" $\tilde{X}$.
Now I've been interested in the connection between information equilibrium, economics, and machine learning (e.g. GAN's real data, generated data, and discriminator have a formal similarity to information equilibrium's information source, information destination, and detector — the latter I use as a possible way of understanding of demand, supply, and price on this blog). I'm always on the lookout for connections to information equilibrium. This is a work in progress, but I first thought it might be valuable to understand information equilibrium in terms of mutual information.
If we have two random variables $X$ and $Y$, then information equilibrium is the condition that:
H(X) = H(Y)
$$
Without loss of generality, we can identify $X$ as the information source (effectively a sign convention) and say in general:
H(X) \geq H(Y)
$$
We can say mutual information is maximized when $Y = f(X)$. The diagram above represents a "noisy" case where either noise (or another random variable) contributes to $H(Y)$ (i.e. $Y = f(X) + n$). Mutual information cannot be greater than the information in $X$ or $Y$. And if we assert a simple case of information equilibrium (with information transfer index $k = 1$), e.g.:
p_{xy} = p_{x}\delta_{xy} = p_{y}\delta_{xy}
$$
then
$$
\begin{align}
I(X ; Y) & = \sum_{x} \sum_{y} p_{xy} \log \frac{p_{xy}}{p_{x}p_{y}}\\
& = \sum_{x} \sum_{y} p_{x} \delta_{xy} \log \frac{p_{x} \delta_{xy} }{p_{x}p_{y}}\\
& = \sum_{x} \sum_{y} p_{x} \delta_{xy} \log \frac{\delta_{xy} }{p_{y}}\\
& = \sum_{x} p_{x} \log \frac{1}{p_{x}}\\
& = -\sum_{x} p_{x} \log p_{x}\\
& = H(X)
\end{align}
$$
Note that in the above, the information transfer index accounts for the "mismatch" in dimensionality in the Kronecker delta (i.e. a die roll that determines the outcome of a coin flip such that a roll of 1, 2, or 3 yields heads and 4, 5, or 6 yields tails).
Basically, information equilibrium is the case where $H(X)$ and $H(Y)$ overlap, $Y = f(X)$, and mutual information is maximized.
Thursday, September 21, 2017
My introductory chapter on economics
I was reading the new CORE economics textbook. It starts off with some bold type stating "capitalism revolutionized the way we live", effectively defining economics as the study of capitalism as well as "other economic systems". The first date in the first bullet point is the 1700s (the first sentence mentions an Islamic scholar of the 1300s discussing India). This started me thinking: how would I start an economics textbook based on the information-theoretic approach I've been working on?
...
An envelope-tablet (bulla) and tokens ca. 4000-3000 BCE from the Louvre.
© Marie-Lan Nguyen / Wikimedia Commons
© Marie-Lan Nguyen / Wikimedia Commons
Commerce and information
While she was studying the uses of clay before the development of pottery in Mesopotamian culture in the early 1970s, Denise Schmandt-Besserat kept encountering small dried clay objects in various shapes and sizes. They were labelled with names like "enigmatic objects" at the time because there was no consensus theory of what they were. Schmandt-Besserat first cataloged them as "geometric objects" because they resembled cones and disks, until ones resembling animals and tools began to emerge. Realizing they might have symbolic purpose, she started calling them tokens. That is what they are called today.
The tokens appear in the archaeological record as far back as 8000 BCE, and there is evidence they were fired which would make them some of the earliest fired ceramics known. They appear all over Iran, Iraq, Syria, Turkey, and Israel. Most of this was already evident, but unexplained, when Schmandt-Besserat began her work. Awareness of the existence of tokens, in fact, went back almost all the way to the beginning of archaeology in the nineteenth century.
Tokens were found inside one particular "envelope-tablet" (hollow cylinders or balls of clay — called bullae) found in the 1920s at a site near ancient Babylon. It had a cuneiform inscription on the outside that read: "Counters representing small cattle: 21 ewes that lamb, 6 female lambs... " and so on until 49 animals were described. The bulla turned out to contain 49 tokens.
In a 1966 paper Pierre Amiet suggested the tokens represented specific commodities, citing this discovery of 49 tokens and the speculation that the objects were part of an accounting system or other record-keeping. Similar systems are used to this day. For example, in parts of Iraq pebbles are used as counters to keep track of sheep.
But because this was the only such envelope-tablet known, it seemed a stretch to reconstruct a entire system of token-counting based on one single piece of evidence. But, as Schmandt-Besserat later noted, the existence of many tokens having the same shape but in different sizes is suggestive that they belonged to an accounting system of some sort. With no further evidence however, this theory remained just one possible explanation for the function of the older tokens that pre-dated writing.
In 2013, fresh evidence emerged from bullae dated to ca. 3300 BCE. Through use of CT scanning and 3D modelling to see inside unbroken clay balls, researchers discovered that the bullae contained a variety of geometric shapes consistent with Schmandt-Besserat's tokens.
CT scan of Choga Mish bulla and Denise Schmandt-Besserat
While these artifacts were of great interest in Schmandt-Besserat's hypothesis about the origin of writing, they fundamentally represent economic archaeological artifacts.
Could a system function with just a single type of token? Cowrie shells seemed to provide a similar accounting function around the Pacific and Indian oceans (because of this, the Latin name of the specific species is Monetaria moneta, "the money cowrie"). The distinctive cowrie shape was even cast in copper and bronze in China as early as 700 BCE, making it an early form of metal coinage. The earliest known metal coins along the Mediterranean come from Lydia from before 500 BCE.
Bronze cowrie shells from the Shang dynasty (1600-1100 BCE)
The 2013 study of the Mesopotamian bullae was touted in the press as the "very first data storage system", and (given the probability distributions of finding various tokens) a bulla containing a particular set of tokens represents a specific amount of information by Claude Shannon's definition in his 1948 paper establishing information theory.
In this light, commerce can be seen as an information processing system whose emergence is deeply entwined with the emergence of civilization. It is also deeply entwined with modern mathematics.
Fibonacci today is most associated with the Fibonacci sequence of integers. His Liber Abaci ("Book of Calculation", 1202) introduced Europe to Hindu-Arabic numerals in its first section, and in the second section illustrated the usefulness of these numerals (instead of the Roman numerals used at the time) to businessmen in Pisa with examples of calculations involving currency, profit, and interest. In fact, Fibonacci's work spread back into Arabic business as the Arabic numerals had mostly been used by Arabic astronomers and scientists.
The accouting system and other economic data is often described using these numerals today — at least where they need to be accessed by humans. In reality, the vast majority of commerce is conducted using abstract bullae that either contain a token or not: bits. These on/off states (bullae that contain a token or not) that are the fundamental units of information theory also represent the billions of transactions and other information flowing from person to person or firm to firm.
At its heart, economics is the study of this information processing system.
...
Update: See also Eric Lonergan's fun blog experiment (click on the last link) on money and language. Additionally, Kocherlakota's Money is Memory [pdf] is relevant.
Credits:
I took liberally (maybe too liberally) from the first link here, and added to it.
http://sites.utexas.edu/dsb/tokens/
https://oi.uchicago.edu/sites/oi.uchicago.edu/files/uploads/shared/docs/nn215.pdf
Wednesday, September 20, 2017
Dynamic equilibrium versus the Federal Reserve
The Fed is out with its forecast from its September meeting, and it effectively projects constant inflation and unemployment over the next several years. One thing that I did think was interesting is that if the Fed forecast is correct, then the dynamic equilibrium recession detection algorithm would predict a recession in 2019 (which is where it currently forecasts one unless the unemployment rate continues to fall):
This happens to be where the two forecasts diverge (the dynamic equilibrium model is a conditional forecast in the counterfactual world where there is no recession in the next several years [1]).
Here is an update versus the FRBSF forecast as well (post-forecast data in black):
...
Footnotes:
[1] While it can't predict the timing of a recession, it does predict the form: the data will rise several percent above the path (depending on the size of the recession) continuing the characteristic "stair-step" appearance of the log-linear transform of the data:
Tuesday, September 19, 2017
Information, real, nominal, and Solow
John Handley has the issue that anyone with a critical eye has about the Solow model's standard production function and total factor productivity: it doesn't make sense once you start to compare countries or think about what the numbers actually mean.
My feeling is that the answer to this in economic academia is a combination of "it's a simple model, so it's not supposed to stand up to scrutiny" and "it works well enough for an economic model". Dietz Vollrath essentially makes the latter point (i.e. the Kaldor facts, which can be used to define the Solow production function, aren't rejected) in his pair of posts on the balanced growth path that I discuss in this post.
I think the Solow production function represents an excellent example of how biased thinking can lead you down the wrong path; I will attempt to illustrate the implicit assumptions about production that go into its formulation. This thinking leads to the invention of "total factor productivity" to account for the fact that the straitjacket we applied to the production function (for the purpose of explaining growth, by the way) makes it unable to explain growth.
Let's start with the last constraint applied to the Cobb-Douglas production function: constant returns to scale. Solow doesn't really explain it so much as assert it in his paper:
Output is to be understood as net output after making good the depreciation of capital. About production all we will say at the moment is that it shows constant returns to scale. Hence the production function is homogeneous of first degree. This amounts to assuming that there is no scarce nonaugmentable resource like land. Constant returns to scale seems the natural assumption to make in a theory of growth.
Solow (1956)
But constant returns to scale is frequently justified by "replication arguments": if you double the factory machines (capital) and the people working them (labor), you double output.
Already there's a bit of a 19th century mindset going in here: constant returns to scale might be true to a decent approximation for drilling holes in pieces of wood with drill presses. But it is not obviously true of computers and employees: after a certain point, you need an IT department to handle network traffic, bulk data storage, and software interactions.
But another reason we think constant returns to scale is a good assumption also involves a bit of competition: firms that have decreasing returns to scale must be doing something wrong (e.g. poor management), and therefore will lose out in competition. Increasing returns to scale is a kind of "free lunch" that also shouldn't happen.
Underlying this, however, is that Solow's Cobb-Douglas production function is thought of in real terms: actual people drilling actual holes in actual pieces of wood with actual drill presses. But capital is bought, labor is paid, and output is sold with nominal dollars. While some firms might adjust for inflation in their forecasts, I am certain that not every firm makes production decisions in real terms. In a sense, in order to have a production function in terms of real quantities, we must also have rational agents computing the real value of labor and capital, adjusting for inflation.
The striking thing is that if we instead think in nominal terms, the argument about constant returns to scale falls apart. If you double the nominal value of capital (going from 1 million dollars worth of drill presses to 2 million) and the labor force, there is no particular reason that nominal output has to double.
Going from 1 million dollars worth of drill presses to 2 million dollars at constant prices means doubling the number of drill presses. If done in a short enough period of time, inflation doesn't matter. In that case, there is no difference in the replication argument using real or nominal quantities. But here's where we see another implicit assumption required to keep the constant returns to scale — there is a difference over a long period of time. Buying 1000 drill presses in 1957 is very different from buying 1000 drill presses in 2017, so doubling them over 60 years is different. But that brings us back to constant returns to scale: constant returns to scale tells us that doubling in 1957 and doubling over 60 years both result in doubled output.
That's where part of the "productivity" is supposed to come in: 1957 vintage drill presses aren't as productive as 2017 drill presses given the same labor input. Therefore we account for these "technological microfoundations" (that seem to be more about engineering than economics) in terms of a growing factor productivity. What comes next requires a bit of math. Let's log-linearize and assume everything grows approximately exponentially (with growth rates $\eta$, $\lambda$, and $\kappa$). Constant returns to scale with constant productivity tells us:
\eta = (1-\alpha) \lambda + \alpha \kappa
$$
Let's add an exponentially growing factor productivity to capital:
\eta = (1-\alpha) \lambda + \alpha (\kappa + \pi_{\kappa})
$$
Now let's re-arrange:
\begin{align}
\eta = & (1-\alpha) \lambda + \alpha \kappa (1 + \pi_{\kappa}/\kappa)\\
= & (1-\alpha) \lambda + \alpha' \kappa
\end{align}
$$
Note that $1 - \alpha + \alpha' \neq 1$. We've now just escaped the straitjacket of constant returns to scale by adding a factor productivity we had to add in order to fit data because of our assumption of constant returns to scale. Since we've given up on constant returns to scale when including productivity, why not just add total factor productivity back in:
\eta = \pi_{TFP} + (1-\alpha) \lambda + \alpha \kappa
$$
let's arbitrarily partition TFP to labor and capital (in half, but doesn't matter). Analogous to the capital productivity, we obtain:
\eta = \beta' \lambda + \alpha' \kappa
$$
with
$$
\begin{align}
\beta' = & (1 - \alpha) + \pi_{TFP}/(2 \lambda)\\
\alpha' = & \alpha + \pi_{TFP}/(2 \kappa)
\end{align}
$$
In fact, if we ignore constant returns to scale and allow nominal quantities (because you're no longer talking about the constant returns to scale of real quantities) you actually get a pretty good fit with constant total factor productivity [1]:
Now I didn't just come by this because I carefully thought out the argument against using constant returns to scale and real quantities. Before I changed my paradigm, I was as insistent on using real quantities as any economist.
What changed was that I tried looking at economics using information theory. In that framework, economic forces are about communicating signals and matching supply and demand in transactions. People do not buy things in real dollars, but in nominal dollars. Therefore those signals are going to be in terms of nominal quantities.
And this comes to our final assumption underlying the Solow model: that nominal price and the real value of a good are separable. Transforming nominal variables into real ones by dividing by the price level is taken for granted. It's true that you can always mathematically assert:
N = PY
$$
But if $N$ represents a quantity of information about the goods and services consumed in a particular year, and $Y$ is supposed to represent effectively that same information (since nominal and real don't matter at a single point in time), can we really just divide $N$ by $P$? Can I separate the five dollars from the cup of coffee in a five dollar cup of coffee? The transaction events of purchasing coffee happen in units of five dollar cups of coffee. At another time, they happened in one dollar cups of coffee. But asserting that the "five dollar" and the "one dollar" can be removed such that we can just talk about cups of coffee (or rather "one 1980 dollar cups of coffee") is saying something about where the information resides: using real quantities tell us its in the cups of coffee, not the five dollars or in the holistic transaction of a five dollar cup of coffee.
Underlying this is an assumption about what inflation is: if the nominal price is separable, then inflation is just the growth of a generic scale factor. Coffee costs five dollars today rather than the one dollar it cost in 1980 because prices rose by about a factor of five. And those prices rise for some reason unrelated to cups of coffee (perhaps monetary policy). This might make some sense for an individual good like a cup of coffee, but it is nonsense for an entire economy. GDP is 18 trillion dollars today rather than 3 trillion in 1980 because while the economy grew by factor of 2, prices grew by a factor of 3 for reasons unrelated to the economy growing by a factor of 2 or changes in the goods actually produced?
To put this mathematically, when we assume the price is separable, we assume that we don't have a scenario where [2]
N = P(Y) Y(P)
$$
because in that case, the separation doesn't make any sense.
One thing I'd like to emphasize is that I'm not saying these assumptions are wrong, but rather that they are assumptions — assumptions that didn't have to be made, or made in a particular way.
The end result of all these assumptions — assumptions about rational agents, about the nature of inflation, about where the information resides in a transaction, about constant returns to scale — led us down a path towards a production function where we have to invent a new mysterious fudge factor we call total factor productivity in order to match data. And it's a fudge factor that essentially undoes all the work being done by those assumptions. And it's for no reason because the Cobb-Douglas production function, which originally didn't have a varying TFP by the way, does a fine job with nominal quantities, increasing returns to scale, and a constant TFP as shown above.
It's one of the more maddening things I've encountered in my time as a dilettante in economic theory. Incidentally, this all started when Handley asked me on Twitter what the information equilibrium approach had to say about growth economics. Solow represents a starting point of growth economics, so I feel a bit like Danny in The Shining approaching the rest of the field:
...
Update #1: 20 September 2017
John Handley has a response:
Namely, [Smith] questions the attachment to constant returns to scale in the Solow model, which made me realize (or at least clarified my thinking about the fact that) growth theory is really all about increasing returns to scale.
That's partially why it is so maddening to me. Contra Solow's claim that constant returns to scale is "the natural assumption", it is in fact the most unnatural assumption to make in a theory of economic growth.
Update #2: 20 September 2017
Sri brings up a great point on Twitter from the history of economics — that this post touches on the so-called "index number problem" and the "Cambridge capital controversy". I actually have posts on resolving both using information equilibrium (INP and CCC, with the latter being a more humorous take). However, this post intended to communicate that the INP is irrelevant to growth economics in terms of nominal quantities, and that empirically there doesn't seem to be anything wrong with adding up capital in terms of nominal value. The CCC was about adding real capital (i.e. espresso machines and drill presses) which is precisely Joan Robinson's "adding apples and oranges" problem. However, using nominal value of capital renders this debate moot as it becomes a modelling choice and shifts the "burden of proof" to comparison with empirical data.
Much like how the assumptions behind the production function lead you down the path of inventing a "total factor productivity" fudge factor because the model doesn't agree with data on its own, they lead you to additional theoretical problems such as the index number problem and Cambridge capital controversy.
Footnotes:
[1] Model details and the Mathematica code can be found on GitHub in my informationequilibrium repository.
[2] Funny enough, the information equilibrium approach does mix these quantities in a particular way. We'd say:
$$
\begin{align}
N = & \frac{1}{k} P Y\\
= & \frac{1}{k} \frac{dN}{dY} Y
\end{align}
$$
or in the notation I show $N = P(Y) Y$.
Monday, September 18, 2017
Ideal and non-ideal information transfer and demand curves
I created an animation to show how important the assumption of fully exploring the state space (ideal information transfer i.e. information equilibrium) is to "emergent" supply and demand. In the first case, we satisfy the ideal information transfer requirement that agent samples from the state space accurately reproduce that state space as the number of samples becomes large:
This is essentially what I described in this post, but now with an animation. However, if agents "bunch up" in one part of state space (non-ideal information transfer), then you don't get a demand curve:
Sunday, September 17, 2017
Marking my S&P 500 forecast to market
Here's an update on how the S&P 500 forecast is doing (progressively zooming out in time):
Before people say that I'm just validating a log-linear forecast, it helps to understand that the dynamic equilibrium model says not just that in the absence of shocks the path of a "price" will be log-linear, but will also have the same log-linear slope before and after those shocks. A general log-linear stochastic projection will have two parameters (a slope and a level) [1], the dynamic equilibrium model has one. This is the same as saying the data will have a characteristic "stair-step" appearance [2] after a log-linear transformation (taking the log and subtracting a line of constant slope).
[1] An ARIMA model will also have a scale that defines the rate of approach to that log-linear projection. More complex versions will also have scales that define the fluctuations.
[2] For the S&P 500, it looks like this (steps go up or down, and in fact exhibit a bit of self-similarity at different scales):
Friday, September 15, 2017
The long trend in energy consumption
I came across this from Steve Keen on physics and economics, where he says:
... both [neoclassical economists and Post Keynesians] ignore the shared weakness that their models of production imply that output can be produced without using energy—or that energy can be treated as just a form of capital. Both statements are categorically false according to the Laws of Thermodynamics, which ... cannot be broken.
He then quotes Eddington, ending with "But if your theory is found to be against the second law of thermodynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation." After this, Keen adds:
Arguably therefore, the production functions used in economic theory—whether spouted by mainstream Neoclassical or non-orthodox Post Keynesians—deserve to "collapse in deepest humiliation".
First, let me say that the second law of thermodynamics applies to closed systems, which the Earth definitely isn't (it receives energy from the sun). But beyond this, I have no idea what Keen is trying to prove here. Regardless of what argument you present, a Cobb-Douglas function cannot be "false" according to thermodynamics because it is just that: a function. It's like saying the Riemann zeta function violates the laws of physics.
The Cobb-Douglas production functions also do not imply output can be produced without energy. The basic one from the Solow model implies labor and capital are inputs. Energy consumption is an implicit variable in both labor and capital. For example, your effective labor depends on people being able to get to work, using energy. But that depends on the distribution of firms and people (which in the US became very dependent on industrial and land use policy). That is to say
Y = A(t) L(f_{1}(E, t), a, b, c ..., t)^{\alpha} K(f_{2}(E, t), x, y, z ..., t)^{\beta}
$$
where $f_{1}$ and $f_{2}$ are complex functions of energy and time. Keen is effectively saying something equivalent to: "Production functions ignore the strong and weak nuclear forces, and therefore violate the laws of physics. Therefore we should incorporate nucleosynthesis in our equations to determine what kinds of metals are available on Earth in what quantities." While technically true, the resulting model is going to be intractable.
The real question you should be asking is whether that Cobb Douglas function fits the data. If it does, then energy must be included implicitly via $f_{1}$ and $f_{2}$. If it doesn't, then maybe you might want to consider questioning the Cobb-Douglas form itself? Maybe you can come up with a Cobb-Douglas function that includes energy as a factor of production. If that fits the data, then great! But in any of the cases, it wasn't because Cobb-Douglas production functions without explicit energy terms violate the laws of physics. They don't.
However, what I'm most interested in comes in at the end. Keen grabs a graph from this blog post by physicist Tom Murphy (who incidentally is a colleague of a friend of mine). Keen's point is that maybe the Solow residual $A(t)$ is actually energy, but doesn't actually make the case except by showing Murphy's graph and waving his hands. I'm actually going to end up making a better case.
Now the issues with Murphy's post in terms of economics were pretty much handled already by Noah Smith. I'd just like to discuss the graph, as well as note that sometimes even physicists can get things wrong. Muphy fits a line to a log plot of energy consumption with a growth rate of 2.9%. I've put his line (red) along with the data (blue) on this graph:
Ignore any caveats about measuring energy consumption in the 17th century and take the data as given. Now immediately we can ask a question of Murphy's model: energy consumption goes up by 2.9% per year regardless of technology from the 1600s to the 2000s? The industrial revolution didn't have any effect?
As you can already see, I tried the dynamic equilibrium model out on this data (green), and achieved a pretty decent fit with four major shocks. They're centered at 1707.35, 1836.93, 1902.07, and 1959.69. My guess is that these shocks are associated with the industrial revolution, railroads, electrification, and the mass production of cars. YMMV. Let's zoom in on the recent data (which is likely better) [1]:
Instead of Murphy's 2.9% growth rate that ignores technology (and gets the data past 1980 wrong by a factor of 2), we have a equilibrium growth rate of 0.5% (which incidentally is about half the US population growth rate during this period). Instead of Muphy's e-folding time of about 33 years, we have an e-folding time of 200 years. Muphy uses the doubling time of 23 years in his post, which becomes 139 years. This pushes boiling the Earth in 400 years (well, at a 2.3% growth rate per Murphy) to about 1850 years.
Now don't take this as some sort of defense of economic growth regardless of environmental impact (the real problem is global warming which is a big problem well before even that 400 year time scale), but rather as a case study where your conclusions depend on how you see the data. Murphy sees just exponential growth; I see technological changes that lead to shocks in energy consumption. The latter view is amenable to solutions (e.g. wind power) while Murphy thinks alternative energy isn't going to help [2].
Speaking of technology, what about Keen's claim that total factor productivity (Solow residual) might be energy? Well, I checked out some data from John Fernald at the SF Fed on productivity (unfortunately I couldn't find the source so I had to digitize the graph at the link) and ran it through the dynamic equilibrium model:
Interestingly the shocks to energy consumption and the shock to TFP line up almost exactly (TFP in 1958.04, energy consumption in 1959.69). The sizes are different (the TFP shock is roughly 1/3 the size of the energy shock in relative terms), and the dynamic equilibria are different (a 0.8% growth rate for TFP). These two pieces of information mean that it is unlikely we can use energy as TFP. The energy shock is too big, but we could fix that by decreasing the Cobb-Douglas exponent of energy. However, we need to increase the Cobb-Douglas exponent in order to match the growth rates making that already-too-big energy shock even bigger.
But the empirical match up between TFP and the energy shock in time is intriguing [3]. It also represents an infinitely better case for including energy in production functions than Keen's argument that they violate the laws of thermodynamics.
Footnotes:
[1] Here is the derivative (Murphy's 2.9% in red, the dynamic equilibrium in gray and the model with the shock in green):
[3] Murphy actually says his conclusion is "independent of technology", but that's only true in the worst sense that his conclusion completely ignores technology. If you include technology (i.e. those shocks in the dynamic equilibrium), the estimate of the equilibrium growth rate falls considerably.
[2] It's not really that intriguing because I'm not sure TFP is really a thing. I've shown that if you look at nominal quantities, Solow's Cobb-Douglas production function is an excellent match to data with a constant TFP. There's no TFP function to explain.
Thursday, September 14, 2017
The long trend in labor hours
Branko Milanovic posted a chart on Twitter showing the average annual hours worked showing, among other things, that people worked twice as many hours during the industrial revolution:
From 1816 to 1851, the number of hours fell by about 0.14% per year:
100 (Log[3185] − Log[3343])/(1851-1816) = − 0.138
This graph made me check out the data on FRED for average working hours (per week, indexed to 2009 = 100). In fact, I checked it out with the dynamic equilibrium model:
Any guess what the dynamic equilibrium rate of decrease is? It's − 0.132% — almost the same rate as in the 1800s! There was a brief period of increased decline (a shock to weekly labor hours centered at 1973.4) that roughly coincides with women entering the workforce and the inflationary period of the 70s (that might be all part of the same effect).
Tuesday, September 12, 2017
Bitcoin update
I wanted to compare the bitcoin forecast to the latest data even though I updated it only last week since according to the model, it should move fast (logarithmic decline of -2.6/y). Even including the "news shock" blip (basically noise) from Jamie Dimon's comments today, the path is on the forecast track:
This is a "conditional" forecast -- it depends on whether there is a major shock (positive or negative, but nearly all have been positive so far for bitcoin).
...
Update 18 September 2017
Over the past week (possibly due to Dimon's comments), bitcoin took a dive. It subsequently recovered to the dynamic equilibrium trend:
...
Update 25 September 2017
Continuing comparison of forecast to data:
...
Update 28 September 2017
Another few days of data:
Update 4 October 2017
Update 9 October 2017
Update 11 October 2017
...
Update 17 October 2017
There appears to have been yet another shock, so I considered this a failure of model usefulness. See more here.
...
Update 18 September 2017
Over the past week (possibly due to Dimon's comments), bitcoin took a dive. It subsequently recovered to the dynamic equilibrium trend:
...
Update 25 September 2017
Continuing comparison of forecast to data:
...
Update 28 September 2017
Another few days of data:
Update 4 October 2017
Update 9 October 2017
Update 11 October 2017
...
Update 17 October 2017
There appears to have been yet another shock, so I considered this a failure of model usefulness. See more here.
JOLTS leading indicators update
New JOLTS data is out today. In a post from a couple of months ago, I noted that the hires data was a bit of a leading indicator for the 2008 recession and so decided to test that hypothesis by tracking it and looking for indications of a recession (i.e. a strong deviation from the model forecast requiring an additional shock — a recession — to explain).
Here is the update with the latest data (black):
This was a bit of mean reversion, but there remains a correlated negative deviation. In fact, most of the data since 2016 ([in gray] and all of the data since the forecast was made [in black]) has been below the model:
That histogram is of the data deviations from the model. However, we still don't see any clear sign of a recession yet — consistent with the recession detection algorithm based on unemployment data.
Monday, September 11, 2017
Search and matching II: theory
I think Claudia Sahm illustrates the issue with economics I describe in Part I with her comments on the approach to models of unemployment. Here are a few of Sahm's tweets:
I was "treated" to over a dozen paper pitches that tweaked a Mortensen-Pissarides [MP] labor search model in different ways, this isn't new ... but it is what science looks like, I appreciate broad summary papers and popular writing that boosts the work but this is a sloooow process ... [to be honest], I've never been blown away by the realism in search models, but our benchmark of voluntary/taste-based unemployment is just weird
Is the benchmark approach successful? If it is, then the lack of realism should make you question what is realistic and therefore the lack of realism of MP shouldn't matter. If it isn't, then why is it the benchmark approach? An unrealistic and unsuccessful approach should have been dropped long ago. Shouldn't you be fine with any other attempt at understanding regardless of realism?
This discussion was started by Noah Smith's blog post on search and matching models of unemployment, which are generally known as Mortensen-Pissarides models (MP). He thinks that they are part of a move towards realism:
Basically, Ljungqvist and Sargent are trying to solve the Shimer Puzzle - the fact that in classic labor search models of the business cycle, productivity shocks aren't big enough to generate the kind of employment fluctuations we see in actual business cycles. ... Labor search-and-matching models still have plenty of unrealistic elements, but they're fundamentally a step in the direction of realism. For one thing, they were made by economists imagining the actual process of workers looking for jobs and companies looking for employees. That's a kind of realism.
One of the unrealistic assumptions MP makes is the assumption of a steady state. Here's Morentsen-Pissarides (1994) [pdf]:
The analysis that follows derives the initial impact of parameter changes on each conditional on current unemployment, u. Obviously, unemployment eventually adjusts to equate the two in steady state. ... the decrease in unemployment induces a fall in job creation (to maintain v/u constant v has to fall when u falls) and an increase in job destruction, until there is convergence to a new steady state, or until there is a new cyclical shock. ... Job creation also rises in this case and eventually there is convergence to a new steady state, where although there is again ambiguity about the final direction of change in unemployment, it is almost certainly the case that unemployment falls towards its new steady-state value after its initial rise.
It's entirely possible that an empirically successful model has a steady state (the information equilibrium model described below asymptotically approaches one at u = 0%), but a quick look at the data (even data available in 1994) shows us this is an unrealistic assumption:
Is there a different steady state after every recession? Yet this particular assumption is never mentioned (in any of the commentary) and we have e.g. lack of heterogeneity as the go-to example from Stephen Williamson:
Typical Mortensen-Pissarides is hardly realistic. Where do I see the matching function in reality? Isn't there heterogeneity across workers, and across firms in reality? Where are the banks? Where are the cows? It's good that you like search models, but that can't be because they're "realistic."
Even Roger Farmer only goes so far as to say there are multiple steady states (multiple equilibria, using a similar competitive search [pdf] and matching framework). Again, it may well be that an empirically successful model will have one or more steady states, but if we're decrying the lack of realism of the assumptions shouldn't we decry this one?
I am going to construct the information equilibrium approach to unemployment trying to be explicit and realistic about my assumptions. But a key point I want to make here is that "realistic" doesn't necessarily mean "explicitly represent the actions of agents" (Noah Smith's "pool players arm"), but rather "realistic about our ignorance".
What follows is essentially a repeat of this post, but with more discussion of methodology along the way.
Let's start with an assumption that the information required to specify the economic state in terms of the number of hires ($H$) is equivalent to the information required to specify the economic state in terms of the number of job vacancies ($V$) when that economy is in equilibrium. Effectively we are saying there are, for example, two vacancies for every hire (more technically we are saying that the information associated with the probability of two vacancies is equal to the information associated with the probability of a single hire). Some math lets us then say:
\text{(1) } \; \frac{dH}{dV} = k_{v} \; \frac{H}{V}
$$
This is completely general in the sense that we don't really need to understand the details of the underlying process, only that the agents fully explore every state in the available state space. We're assuming ignorance here and putting forward the most general definition of equilibrium consistent with conservation of information and scale invariance (i.e. doubling $H$ and $V$ gives us the same result).
If we have a population that grows a few percent a year, we can say our variables are proportional to an exponential function. If $V \sim \exp v t$ with growth rate $v$, then according to equation (1) above $H \sim \exp k_{v} v t$ and (in equilibrium):
\frac{d}{dt} \log \frac{H}{V} \simeq (k_{v} - 1) v
$$
When the economy is in equilibrium (a scope condition), we should have lines of constant slope if we plot the time series $\log H/V$. And we do:
This is what I've called a "dynamic equilibrium". The steady state of an economy is not e.g. some constant rate of hires, but rather more general — a constant decrease (or increase) in $H/V$. However the available data does not appear to be equilibrium data alone. If the agents fail to fully explore the state space (for example, firms have correlated behavior where they all reduce the number of hires simultaneously), we will get violations of the constant slope we have in equilibrium.
In general it would be completely ad hoc to declare "2001 and 2008 are different" were it not for other knowledge about the years 2001 and 2008: they are the years of the two recessions in the data. Since we don't know much about the shocks to the dynamic equilibrium, let's just say they are roughly Gaussian in time (start of small, reach a peak, and then fall off). Another way to put this is that if we subtract the log-linear slope of the dynamic equilibrium, the resulting data should appear to be logistic step functions:
The blue line shows the fit of the data to this model with 90% confidence intervals for the single prediction errors. Transforming this back to the original data representation gives us a decent model of $H/V$:
Now employment isn't just vacancies that are turned into hires: there have to be unemployed people to match with vacancies. Therefore there should also be a dynamic equilibrium using hires and unemployed people ($U$). And there is:
Actually, we can rewrite our information equilibrium condition for two "factors of production" and obtain the Cobb-Douglas form (solving a pair of partial differential equations like Eq. (1) above):
H(U, V) = a U^{k_{u}} V^{k_{v}}
$$
This is effectively a matching function (not the same as in the MP paper, but discussed in e.g. Petrongolo and Pissarides (2001) [pdf]). We should be able to fit this function to the data, but it doesn't quite:
Now this should work fine if the shocks to $H/U$ and shocks to $H/V$ are all the shocks. However it looks like we acquire a constant error coming through the 2008 recession:
Again, it makes sense to call the recession a disequilibrium process. This means there are additional shocks to the matching function itself in addition to the shocks to $H/U$ and $H/V$. We'd interpret this as a recession representing a combination of fewer job postings, fewer hires per available worker, as well as fewer matches given openings and available workers. We could probably work out some plausible psychological story (unemployed workers during a recession are seen as not as desirable by firms, firms are reticent to post jobs, and firms are more reticent to hire for a given posting). You could probably write up a model where firms suddenly become more risk averse during a recession. However you'd need many, many recessions in order to begin to understand if recessions have any commonalities.
Another way to put this is that given the limited data, it is impossible to specify the underlying details of the dynamics of the matching function during a recession. During "normal times", the matching function is boring — it's fully specified by a couple of constants. All of your heterogeneous agent dynamics "integrate out" (i.e. aggregate) into a couple of numbers. The only data that is available to work out agent details is during recessions. The JOLTS data used above has only been recorded since 2000, leaving only about 30 monthly measurements taken during two recessions to figure out a detailed agent model. At best, you could expect about 3 parameters (which is in fact how many parameters are used in the Gaussian shocks) before over-fitting sets in.
But what about heterogenous agents (as Stephen Williamson mentions in his comment on Noah Smith's blog post)? Well, the information equilibrium approach generalizes to ensembles of information equilibrium relationships such that we basically obtain
H_{i}(U_{i}, V_{i}) = a U_{i}^{\langle k_{u} \rangle} V_{i}^{\langle k_{v} \rangle}
$$
where $\langle k \rangle$ represents an ensemble average over different firms. In fact, the $\langle k \rangle$ might change slowly over time (roughly the growth scale of the population, but it's logarithmic so it's a very slow process). The final matching function is just a product over different types of labor indexed by $i$:
H(U, V) = \prod_{i} H_{i}(U_{i}, V_{i})
$$
Given that the information equilibrium model with a single type of labor for a single firm appears to explain the data about as well as it can be explained, adding heterogenous agents to this problem serves only to reduce information criterion metrics for explanation of empirical data. That is to say Williamson's suggestion is worse than useless because it makes us dumber about the economy.
And this is a general issue I have with economists not "leaning over backward" to reject their intuitions. Because we are humans, we have a strong intuition that tells us our decision-making should have a strong effect on economic outcomes. We feel like we make economic decisions. I've participated in both sides of the interview process, and I strongly feel like the decisions I made contributed to whether the candidate was hired. They probably did! But millions of complex hiring decisions at the scale of the aggregate economy seem to just average out to roughly a constant rate of hiring per vacancy. Noah Smith, Claudia Sahm, and Stephen Williamson (as well as the vast majority of mainstream and heterodox economists) all seem to see "more realistic" being equivalent to "adding parameters". But if realism isn't being measured by accuracy and information content compared to empirical data, "more realistic" starts to mean "adding parameters for no reason". Sometimes "more realistic" should mean a more realistic understanding of our own limitations as theorists.
It is possible those additional parameters might help to explain microeconomic data (as Noah mentions in his post, this is "most of the available data"). However, since the macro model appears to be well described by only a few parameters, this implies a constraint on your micro model: if you aggregate it, all of the extra parameters should "integrate out" to single parameter in equilibrium. If they do not, they represent observable degrees of freedom that are for some reason not observed. This need to agree with not just the empirical data but its information content (i.e. not have too many parameters than are observable at the macro scale) represents "macrofoundations" for your micro model. But given the available macro data, leaning over backwards requires us to give up on models of unemployment and matching that have more than a couple parameters — even if they aren't rejected.
Subscribe to:
Posts (Atom)