Last night through this morning, I butted into an exchange on Twitter about the flow of money between Steve Roth and Noah Smith (who promptly booted me from whatever strange nonsense he wanted to blather on about ... you can't send a signal with wavefunction collapse and it has nothing to do with money flow [economists: stop talking about quantum mechanics]). It brings up some interesting points. Steve started with the observation that money appears to teleport from one account to another -- there is no "flow" per se. Noah said this was just like water which I assume was an attempt at Ken M style trolling because it makes no sense.
Anyway, here is an animation of dots being instantly debited from one account (box) and credited to another; I know because I wrote the Mathematica code that does it (feel free to email me via the box on the sidebar for a copy):
It's from this post. There is strict accounting (the number of dots is constant, and one dot taken from one box is exactly matched by a dot added to another). Then Steve asked the question that you'd hope to get if you were teaching this stuff as a class:
Which raises the interesting (for me...) Q: when I send you money, how far does it "move"?
This is an interesting question and in the animation above there is an explicit answer: it moves one box in one time step. In real life, if you gave several people a large amount of money, you could measure how fast it moves from one node in the network to another. One bought dinner here; another bought a record there. The restaurant and music store paid their employees the next Thursday, but the wait staff took home their tips that night and one picked up some groceries. It possibly changed forms during this journey from cash from an ATM or a deposit at one. This data would be an input to a bottoms-up measurement of money velocity.
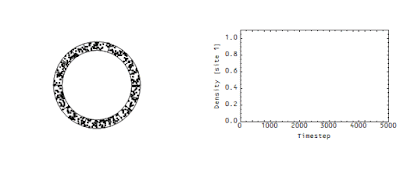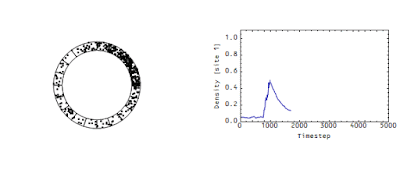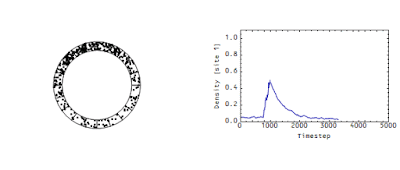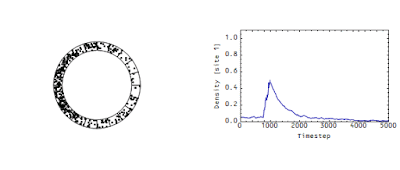
These measurements determine the flow rate of money in an economy analogous to the flow rate of the wave in the animation above. There's another picture from that same post -- it shows the density at a single site:
Note that there's a "decay constant" (of about 500 time steps) -- this decay constant is directly related to the speed of the flow in the first animation. The faster that wave moves in the first animation, the faster the density would decay in the second animation.
I hesitate to bring it up again, but this is exactly what I was talking about when I criticized stock-flow consistent models (Steve also brought up "accounting" approaches).
Even though the accounting is exact in the model above, I could make the wave travel faster or slower (and therefore the decay happen faster or slower) by changing the size of the debits and credits or changing the number of transactions per time step. The velocity of the wave is a free parameter not established by pure accounting. In the linked post, I called that free parameter Γ and was promptly attacked by the stock-flow consistent community for heresy.
So where does this parameter come from? Where does velocity come from? Where does my freedom come from when Nick Rowe says:
But velocity is not just an accounting relationship between flows and stocks. I can choose the velocity of circulation of the money I hold.
Let's consider a set of accounts on a network: I buy something from you, you buy something from someone else, etc. all in a chain (time steps t are vertical, and accounts a are horizontal):
Now, what happens if I do this:
I made the accounts farther apart and the time steps closer together. In terms of accounting? I did nothing. It's just a graphic design choice. That's because these accounting boxes have nothing to do with each other in time and space. However, I've implicitly related them to each other because the boxes "next to" each other are in a sense closer to each other. There is some kind of "connection" between boxes (two are shown in blue):
How do I measure distance diagonally? How is one time step related to one account step? Well, much like how I could make any graphic design choice, I can choose any relationship between a time step Δt and an accounting step Δa (I could even make Δa = Δa(t) change as a function of time -- an expanding accounting universe). There's a free parameter that comes out of this two-dimensional space time (for flat space). In physics, it's called the speed of light (c). The space steps Δx are related to time steps Δt such that distance Δs is measured with some function
Δs² = f(Δx, c Δt) = c² Δt² - Δx²
This is what was so frustrating about the stock-flow argument. The metric was assumed to be analogous to
Δs² = f(Δx, c Δt) = Δt² + Δx²
as if it was a fundamental accounting error to assume otherwise. Frequently physicists do assume h = c = 1. But then we measure everything in terms of energy or distance. One Fermi is not just a distance but also a time and both are the same as 1/197 MeV (inverse energy) which is also about 1/400 electron masses. That's only because the theory of relativity exists relating energy, matter, space, and time. You could do this in stock flow models -- assuming a new fundamental constant Γ = 1 dollar/quarter -- but then you'd have to measure time in terms of money. A year is not 4 quarters, but rather 4 dollars-1.
Stock flow consistent analysis is not the special relativity of economics and there is no such fundamental constant as Γ. The accounting "metric" changes over time (those time steps can seem pretty fast when there's a recession happening).




Jason,
ReplyDeleteThis isn't related to the topic on hand, but i thought you would enjoy the latest release from the SL Fed.
https://www.stlouisfed.org/~/media/Files/PDFs/Bullard/papers/Regime-Switching-Forecasts-17June2016.pdf
I found some similarities in the paper with your characterization of dither in economics. The paper is a stunning departure from the prevailing MP framework. I found it bold and incisive.
Check it out,
-eli
I will check it out; thanks.
DeleteAll sounds very interesting, but I have some doubts:
ReplyDelete"This is an interesting question and in the animation above there is an explicit answer: it moves one box in one time step."
What is a "box"? Is it a person (as in "if you gave several people a large amount of money")? Is it an account (as in "Let's consider a set of accounts on a network")? If I transfer money from my cheque account and into my savings accounts, was there a flow? The fortnight pay deposited in the joint cheque account, did it flow for me, or for my better half -- hi, Lucy Fair, darling, if you are reading this!
Whatever they are, there may be a way to say that Box2 (say, me/my account) is located on an intermediate position between Box1 (you/your account) and Box3 (Steve/his account), but it's not obvious to me. At times, that could be true; most of the time I'd say there is no relationship whatsoever between any of us/our accounts: the space of people/accounts/boxes doesn't seem to be structured.
What, exactly, is the "flow"? Say, you want a can of Coke; you go into a shop, grab it and hand the shop attendant a $20 bill. The attendant gives you the change. Was there a single flow (for the price of the can) or two flows (the $20 and the change)? If there is only one flow, then obviously money flows one way; if there are two flows, won't money flow in both directions?
Equally important: whatever happened to the can of Coke flow (there was a can flow, right?)? Is that taken into account in either your or the SFC framewoks?
B.L. Zebub
Going back to this:
Delete"This is an interesting question and in the animation above there is an explicit answer: it moves one box in one time step."
By the way, I should ask another thing: what is the time step? Is it the time it takes to make the next transaction in a chain of transactions (as it seems suggested by the passage above), or does it have a fixed length?
I don't mean to imply your ideas have no value; but there seem to be many things unclear.
B.L. Zebub
I agree that real life is more complex, but that complexity does not change the underlying concept.
DeleteFirst, if we are considering the space and time structure of the network of nodes (boxes, accounts, businesses, whatever) it is actually static. Imagine the film strip of your life -- were it to be made, it would be a temporal timeline turned into a spatial timeline.
So really we are considering something that could be represented as a purely spatial network. Times are just other points in an abstract "space".
Once we have this network, all we need is a sense in which some nodes are farther away from each other. I shop at the grocery store near where I live, but might never shop at the one near where you live. Even though we are connected via the Internet right now, without some additional work you can't send me money.
Once we have that network and a concept of distance (metric) we have all the necessary elements to the discussion above. Other details are there to make the example more concrete (I didn't want to make my point in terms of an abstract metric d on a network N, but it is possible -- basically if d is a metric on N, so is a • d, so you have a degree of freedom a -- was that illuminating?)
The idea of what a node or a time step is will be an empirical (and possibly changing as I note above) model parameter.
Does the difference between group and phase velocity enter into this discussion?
ReplyDeleteThat is a good analogy.
DeleteIn a sense the phase velocity is "infinite" or just super fast velocity of the dots and the group velocity is the slower velocity of the wave.
We could probably construct a wave packet description as well.
What's fun is to make the flow around the annulus reverse direction. This can be done with some concentration.
ReplyDeleteYes!
DeleteI am in stupefaction of your mathefaction (mathefiction ?).
ReplyDeleteSurely the velocity in question is a social construct (humans decide when to do stuff) and is therefore inscrutable to your analysis. Can you apply maths to random human thoughts?
That velocity depends on human behavior is exactly the point. There is a freedom for velocity to be different and changing. I am arguing against velocity being defined by accounting and constant.
DeleteAnd yes, if there are a sufficient number of people, you can. See FiveThirtyEight or the Princeton Election Consortium for predicting the outcomes of elections based almost entirely on demographics and polling data.
Just because you haven't figured out how to apply math to human behavior (not claiming that I have!) doesn't mean it can't be done. Your failure of imagination is not evidence for or against anything.
This comment has been removed by the author.
ReplyDeleteI agree that velocity is kind of a worthless concept the way most monetarists use it and undermining it will do a great service to humanity if we can throw most of monetarism in the trash heap however I do think the idea of flows, from the PK models, can be helpful. There can be a concept of flows without necessarily trying to determine some natural flow rate and hence some connection to inflation via a supply of money moving around faster and faster
ReplyDeleteAs I understand it flow rate is mostly whatever period we decide to use as a measurement. If I look at my checking account today vs yesterday I see that my numbers changed at the rate of -1000$ in 24 hours.( I had 1000$ net flow out) If I do it over a week the numbers might still only have changed -1000$ and this could be measured as a slower velocity but would be really telling us nothing interesting or useful.
What I think is useful about SFC modeling and PK econ is that it forces one to realize the sources of incomes, savings etc. All my income flows are someone elses spending flows . I do not control my income. None of us do. We are at the mercy of others spending. So I also dont control my savings (stock) I may have a desire to save 12000$ a year but for me to have 1000$ month left over, many things beyond my control must line up and in the face of general econ contraction they will not. If I think the prescription (for me) to spend less to have my extra thousand to save at months end will be sound advice for everyone, I am a fool.
Expansionary austerity is an absolute joke in PK econ. Its also a joke in real life
"If I do it over a week the numbers might still only have changed -1000$ and this could be measured as a slower velocity but would be really telling us nothing interesting or useful."
DeleteBut it does tell us something! If velocity falls as Δt gets bigger, that tells me either no other transactions happened or ΔM(Δt) ~ Δt^a for a < 1.
But really, velocity (like say pressure or temperature) isn't a property of a single transaction (a single atom), but a collective property of thousands of transactions. If you look at the wave in the animation at the top of this post -- it doesn't exist for a single dot.
The problem with "velocity" in monetary theories is that it should be constrained by a model. Constant velocity is an excellent model -- it's just not true. Here's a model that does better.
Yes "austerity" is a terrible idea, but you don't need SFC or PK econ to reach that conclusion. Standard econ comes to the same conclusion. So does information equilibrium.
Jason,
ReplyDeleteHere are a list of points that you may miss in your handling economic temporal data.
(1) Economic data and accounting identities are based on "valid time" temporal theory, but not on "transaction time" functional views.
(2) Flow variables are just logic assertions of data aggregation over specific time intervals. Stock variables are also just logic assertions of data aggregation from the beginning to specific time points.
(3) Change of a stock is NOT equal to flow in economic variables.\
(4) Accounting identities are economic specifications like computer program specifications. They are not economic behaviors as program itself.
Peiya,
Delete(1) "Valid time" and "transaction time" are just different functions mapping real number intervals to economic variables X ... i.e. f:[t, t+Δt) → X(t). My discussion above is valid for any such mapping that isn't pathological, so I am not sure of the relevance.
(2) Did you know that continuous real numbers are just logic assertions (with set theory), too? Also, these two definitions just define stock as the integral (or aggregation or sum) of flows via the Riemann-Stieltjes integral.
(3) This does not make logical sense. How can something "change" if there is no time? A change in stock necessarily has some time scale Δt over which it is measured, else it is identically zero.
X(t) - X(t) = 0
X(t+Δt) - X(t) = ΔX
Therefore there is a natural definition of a flow for all changes in stock = ΔX/Δt. Are you telling me I can't access Δt? Why not?
(4) That is the entire point of my post. Accounting tells you nothing about dynamics.
Jason,
ReplyDeleteI address point (3) first. Usually, a stock variable is recursively defined in this form
Stock(t) = Revaluation[Stock(t-1)] + Flow(t)
But be careful, t in Stock(t) represents a specific time-interval [0 t], however, same t in Flow(t) represents a different time interval [t-start, t-end]. Valid time temporal logic is based on time-interval only(not time snapshot).Time t in stock/flow variables always represents some time-intervals, consistent with NIPA/FOFA time-series data. It has no meaning in individual time snapshots and valid-time temporal logic.
For example,
NetWorth(t) = Revaluation[NetWorth(t-1)] + Saving(t)
Saving(t), a flow variable, asserts total saving over a time period t, which is equal to NetWorth(t) - Revaluation[NetWorth(t-1)] by definition. Revaluation[NetWorth(t-1)] means NetWorth(t-1) over current time-interval[0, t].
But Saving(t) is not the same thing in asserting a change in stock variable NetWorth(t) = ΔNetWorth(t) = NetWorth(t)- NetWorth(t-1).
So, it is not a time-scale issue. It is a valid-time issue.
No, this is mathematically inconsistent -- my comment on (3) stands. See here:
Deletehttp://informationtransfereconomics.blogspot.com/2016/06/stock-flow-accounting-with-calculus.html
I address point (4).
ReplyDeleteYes, accounting tells you nothing about dynamics. But it tells you the constraints of dynamics. Behaviors in theoretical models must meet the economic specifications (i.e. accounting identities). Otherwise, theoretical models are economic fiction.
Often, accounting identities describe the constraints among demand-side variables. They can be used for an economic model checker.
For example, from accounting identities, we can derive money demand Md in GDP production flows among sectors. Md is a fixed function of GDP and independent of money supply Ms. Supply-demand equilibrium models such as MV = PQ, IS/LM, etc. do not meet the economic specifications. Accounting identities can tell us M or LM is a fixed constant not a variable or arbitrary function once GDP is given.
Accounting identities are definitions and therefore do not constrain anything except the words and symbols you use to discuss the model.
DeleteThey are either useful definitions or arbitrary definitions. Failure to make an accounting identity hold just means you've mistakenly used two different definitions of something that are inconsistent with each other.
For example MV = PY is an identity. Given P, Y and M, it tells you what V is ... V ≡ PY/M.
Now is this useful? Well, if V is constant, then yes! But it's not. However it could have a particular functional form, which does make it useful.
See this post for a useful definition of V as the ensemble average of transactions thousands of random markets (as well as more on accounting identities).
DeleteMV = PY is not accounting identity!!
Accounting identities are either economic axioms (E=Y or A=L), temporal definitions or derived temporal theorems. No ad-hoc axiomatized equation such as !!!
Accounting identities are specifications about real economic data and can be used for economic models validation.
It is a temporal definition (i.e. a definition, accounting or not)
DeleteV ≡ PY/M
Therefore:
PY = MV
PY= M(PY/M)
PY = PY
1 = 1
However I am not sure what the distinction between accounting identities, axioms, temporal definitions, other definitions and identities buys us.
Note that this is literally true: M2 velocity on FRED is exactly PY/M2.
It is a definition and all accounting identities are definitions, so this is a distinction without a difference.
Yes, this is money supply velocity, but not money demand velocity. IMO, it is not useful/meaningful.
DeleteMoney demand velocity and actual money demand can be estimated from accounting by spending and income flow variables.
Md Vd = P Q is an accounting identity.
Ms V = P Q is not an accounting identity.
"Accounting identities are definitions and therefore do not constrain anything except the words and symbols you use to discuss the model"
DeleteNo, they constrain spending and income flows/stocks in financial and non-financial assets. Equilibrium equations are related to demand and supply.
For example, GDP(spending) = GDI(income). Actual money demand and velocity are calculated from spending-income flows. Various kinds of spending and income data are in the accounting.
Basic economic axiom is "my expense is your income".
Basic finance axiom is "my liability is your asset".
Whole accounting system is built up from these axioms, then definitions and theorems like "GDP = GDI".
No, [accounting identities] constrain spending and income flows/stocks in financial and non-financial assets.
DeleteNO THEY DO NOT.
1. I give you 10 dollars to buy a widget from you, you give 10 dollars to Brian Romanchuk to buy a widget from him, and he gives 10 dollars to me to buy a widget from me.
2. I give you 5 dollars to buy a widget from you, you give 5 dollars to Brian Romanchuk to buy a widget from him, and he gives 5 dollars to me to buy a widget from me.
Accounting is same in both cases. Yet in one case, 10 dollars went around the circle and in the other 5 dollars did.
Accounting does not constrain that flow. Our actual assets and widgets constrain that flow. If I didn't have 10 dollars, I couldn't do #1. If Brian didn't have any widgets, we couldn't do #1 or #2.
In fact the only thing that stops
3. I give you 5 billion dollars to buy a widget from you, you give 5 billion dollars to Brian Romanchuk to buy a widget from him, and he gives 5 billion dollars to me to buy a widget from me.
... is our lack of 5 billion dollars. That has nothing to do with accounting.
GDP=GDI spending/income relationships recording in accounting in this way.
DeleteC+I+G+X-M = WB + NetOperatingSurplus + CFC + Tariffs - Subsides
Assume GDP = 10 dollars from one widget
spending = C = 10 dollars ( only one product )
income = WB(wages) + NetOperatingSurplus + CFC +Tariffs - Subsides = 10 dollars
You see there are different flow variables from spending and income to calculate the production and should have same value.
That is not responsive to the example. "Annual GDP" in the three examples (if that is all that happened in a year) are 30 dollars, 15 dollars and 15 billion dollars, respectively.
DeleteEach accounting flow variable such as C, I, G, ..., etc. has a procedural measurement method. It is similar in physics to use "operational" definition method to define physical units such as kg, ...
DeleteGDP is not counting goods sales. It counts the production, value added part. I assume that only one widget is produced.
DeleteOperational definition determines "value" of kg, however in equations you can deal entirely in terms of mass scales.
DeleteThis has nothing to do with the discussion. Analogy would be that you deny the existence of mass scale so that everything is massless and measured in units of 1/distance.
Instead, you deny the existence of a time scale, so there is no time which which to consider a flow and time is measured in units of 1/money.
"Annual GDP" in the three examples (if that is all that happened in a year) are 10 dollars, 5 dollars and 5 billion dollars.
DeleteI meant this:
DeleteIn order to derive this temporal theorem "GDP=GDI", we need to clearly understand the meanings of flow variables from their measurement methods.
Jason,
ReplyDeleteI address point (2).
In FOFA S tables, we know the semantics and relationships of balance sheet(stock variable) and saving/capital(flow variables) as shown in my point (3) explanation.
In NIPA/FOFA data, stock is not defined as the integral (or aggregation or sum) of flows via the Riemann-Stieltjes integral. It is a recursive definition.
Thus, there are several issues about ΔH = G - T in G&L SFC.
(1) This is not a NIPA/FOFA accounting identity/flow balance
The correct flow variable balance equation is:
A - L = Government Saving(S) - Government Investment (I)
A - L Government Financial Assets - Liabilities over a time-period t
S - I = G + NonG - T. NonG is non-discretionary spending
and G is discretionary spending = government C + government I in GDP calculation(C + I + G + X - M)
(2) There is a stock variable balance equation between government financial assets(FA), liabilities(FL), and non-financial assets(NFA) as follows.
FA(t) - FL(t) = NetWorth(t) - NFA(t)
But A - L is not equal to change in stock financial stock, which is Δ(FA(t) - FL(t)).
In FOFA, we have complete and separate SC and FC balance matrices on pages 1 and 2, but no SFC transaction matrix!!!. All balance equations in G&L SFC transaction matrix are not true accounting identities because of misunderstanding valid-time temporal data and how to derive this accounting identity (GDP = GDI)
C+I+G+X-M = WB + NetOperatingSurplus + CFC + Tariffs.
If there are separate stock and flow balance matrices with nothing connecting them, then the relationship between stock and flow is completely arbitrary and there can be flow dynamics that have nothing to do with stock dynamics -- for example there could be a recession in "flows" but not in "stocks".
DeleteThis is of course absurd, so there is obviously some connection.
See my new post for what that connection is. A flow is necessarily a change in stock over a time scale (or a stock is the integral of a flow over a time scale).
Whether a definition is recursive or not is not relevant.
DeleteAccounting identities can be formalized as an axiomatic logic system. I illustrate here. http://www.pragcap.com/ama/why-has-heterodox-economics-become-orthodox-on-wall-street-has-or-has-not/
This axiomatic system starts two economic axioms, temporal definitions for every terms, and derived temporal theorems.
It is a self-consistent and correct logic system.
Temporal theorems are about constraints between spending and income flows/stocks in financial and non-financial assets. D/S equilibrium equations are behaviors, not temporal theorems. These behavior equations often contradict temporal theorems that you may not aware.
"there can be flow dynamics that have nothing to do with stock dynamics -- for example there could be a recession in "flows" but not in "stocks".
DeleteYou are exactly right. Flow dynamics refers to new stuffs. Stock dynamics refers to existing stuffs.
GDP recession is in flow dynamics. Debt unsustainable is in stock dynamics. Financial instability could be on both.
Text: "The velocity of the wave is a free parameter not established by pure accounting. In the linked post, I called that free parameter Γ and was promptly attacked by the stock-flow consistent community for heresy."
ReplyDeleteExcept that in the round-about the number of dots is constant. If we applied your stock-flow model to the round-about, Γ would determine the rate at which dots are created or destroyed (or added and subtracted from the round-about, if you prefer). Thus, Γ would have no intrinsic relation to the velocity of the dots, although it could under certain circumstances.
This is incorrect. Γ is the decay constant for the single bin in the second animation. The dots are being "destroyed" in one bin (the first one), but are still in the roundabout. And this decay constant is directly related to the velocity of the dots.
DeleteSorry, Jason. In the economy of the G&L simple model, money is actually created and destroyed by government spending and taxation. In your model for that economy Γ affects the rate of creation and destruction of money, not its velocity.
DeleteJason,
DeleteIn G&L's SIM model we have
∆H = G - T
which means that the amount of money in circulation in the economy during any time period is increased by government spending and decreased by government taxation. Or, as they put it, government spending creates money and government taxation destroys money.
In your model we have instead
∆H = Γ(G - T)
which means that Γ is directly related to the change in the amount of money in circulation the economy. There is an indirect relation with the velocity of money, because the velocity of money affects taxes, and, OC, because the amount of money in the economy also affects velocity. In the round-about the number of dots remains the same. By analogy, ∆H = 0.
I have a bit more to say, but it will wait until after your blogging break.
No. Γ is directly related to the number of times money circulates in the economy in a given time period. It would be related to the number of times a typical dot travels around the roundabout in x time periods. In the version of the diagram above, Γ ~ 1/1000 (I can calculate the actual value, but I'm too lazy to look it up right now) -- each dot moves one square on average in 1000 or so time periods.
DeleteYou can test this by looking at the two diagrams and watching how many sites the peak of the wave moves versus how many time steps in the second diagram.