Christiano et al got much more attention than their paper deserved by putting in a few choice lines in it (Dilettantes! Ha!). Several excellent discussions of the paper — in particular this aspect — are available from Jo Mitchell, Brad DeLong (and subsequent comments), and Noah Smith.
I actually want to defend one particular concept in the paper (although as with most attempts at "science" by economists, it comes off as a nefarious simulacrum). This will serve as a starting point to expand on how exactly we derive knowledge from the world around us. The idea of "DSGE experiments" was attacked by DeLong, but I think he misidentifies the problem [1]. Here is Christiano et al:
The only place that we can do experiments is in dynamic stochastic general equilibrium (DSGE) models.
This line was attacked for its apparent mis-use of the word "experiment", as well as the use of "only". It's unscientific! the critics complain. But here's an excerpt from my thesis:
The same parameters do a good job of reproducing the lattice data for several other quark masses, so the extrapolation to the chiral limit shown in Fig. 2.3 is expected to allow a good qualitative comparison with the instanton model and the single Pauli-Villars subtraction used in the self-consistent calculations.
Lattice data. I am referring to output of lattice QCD computations that are somewhat analogous to using e.g. the trapezoid rule to compute integrals as "data" — i.e. the output of observations. Robert Waldman in comments on DeLong's post makes a distinction between hypothesis (science) and conjecture (math) that would rule out this "lattice QCD data" as a result of "lattice QCD experiments". But this distinction is far too strict as it would rule out actual science done by actual scientists (i.e. physicists, e.g. me).
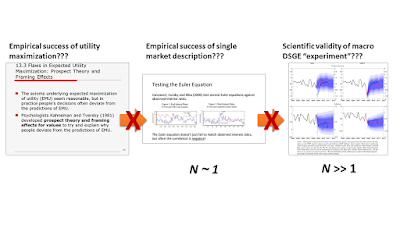
Saying "all simulations derived from theory are just math, not science" misses the nuance provided by understanding how we derive knowledge from the world around us, and lattice QCD provides us with a nice example. The reason we can think of lattice QCD simulations as "experiments" that produce "data" is that we can define a font of scientific validity sourced from empirical success. The framework lattice QCD works with (quantum field theory) has been extensively empirically validated. The actual theory lattice QCD uses (QCD) has been empirically validated at high energy. As such, we can believe the equations of QCD represent some aspect of the world around us, and therefore simulations using them are a potential source of understanding that world. Here's a graphic representing this argument:
Of course, the lattice data could disagree with observations. In that case we'd likely try to understand the error in the assumptions we made in order to produce tractable simulations or possibly limit the scope of QCD (e.g. QCD fails at low energy Q² < 1 Gev²).
The reason the concept of DSGE models as "experiments" is laughable is that it fails every step in this process:
Not only does the underlying framework (utility maximization) disagree with data in many cases, but even the final output of DSGE models also disagrees. The methodology isn't flawed — its execution is.
* * *
The whole dilettantes fracas is a good segue into something I've been meaning to write for awhile now about the sources of knowledge about the real world. I had an extended Twitter argument with Britonomist about whether having a good long think about a system is a scientific source of knowledge about that system (my take: it isn't).
The discussion above represents a particular method of acquiring knowledge about the world around us that I'll call derivation for obvious reasons. Derivation is a logical inference tool: it takes empirically mathematical descriptions of some piece of reality and attempts to "derive" new knowledge about the world. In the case of lattice QCD, we derive some knowledge about the vacuum state based on the empirical success of quantum field theory (math) used to describe e.g. magnetic moments and deep inelastic scattering. The key here is understanding the model under one scope condition well enough that you can motivate its application to others. Derivation uses the empirical validity of the mathematical framework as its source of scientific validity.
Another method is the use of controlled experiments and observation. This is what a lot of people think science is, and it's how it's taught in schools. Controlled experiments can give us information about causality, but one of the key things all forms of observation do is constrain the complexity of what the underlying theory can be through what is sometimes derided as "curve fitting" (regressions). Controlled experiments and observation mostly exclude potential mathematical forms that could be used to describe the data. A wonderful example of this is blackbody radiation in physics. The original experiments basically excluded various simple computations based on Newton's mechanics and Maxwell's electrodynamics. Fitting the blackbody radiation spectrum curve with functional forms of decreasing complexity ultimately led to Planck's single parameter formula that paved the way for quantum mechanics. The key assumption here is essentially Hume's uniformity of nature to varying degrees depending on the degree of control in the experiment. Observation uses its direct connection to empirical reality as its source of scientific validity.
Indifference
A third method is the application of the so-called "principle of indifference" that forms the basis of staticial mechanics in physics and is codified in various "maximum entropy" approaches (such as the one used in the blog). We as theorists plead ignorance of what is "really happening" and just assume what we observe is the most likely configuration of many constituents given various constraints (observational or theoretical). Roderick Dewar has a nice paper explaining how this process is a method of inference giving us knowledge about the world, and not just additional assumptions in a derivation. As mentioned the best example is statistical mechanics: Boltzmann assumed simply that there were lots of atoms underlying matter (which was unknown at the time) and used probability to make conclusions about the most likely states — setting up a framework that accurately describes thermodynamic processes. The key assumption here is that the number of underlying degrees of freedom is large (making our probabilistic conclusions sharper), and "indifference" uses the empirical accuracy of its conclusions as the source of its scientific validity.
Update 2 May 2018: Per the Dewar paper, the idea here is that we observing, explaining, and reproducing empirical regularities without controlling the underlying degrees of freedom which means the details of those degrees of freedom are likely irrelevant. It's kind of the converse of an experiment — if you can't or don't control for a huge number of other variables but still get a reproducible regularity, you likely don't have to control for them. This is why I include it as a separate path from observation.
Update 2 May 2018: Per the Dewar paper, the idea here is that we observing, explaining, and reproducing empirical regularities without controlling the underlying degrees of freedom which means the details of those degrees of freedom are likely irrelevant. It's kind of the converse of an experiment — if you can't or don't control for a huge number of other variables but still get a reproducible regularity, you likely don't have to control for them. This is why I include it as a separate path from observation.
Other paths?
This list isn't meant to be exhaustive, and there are probably other (yet undiscovered!) paths to scientific validity. The main conclusion here is that empirical validity in some capacity is necessary to achieve scientific validity. Philosophizing about a system may well be fun and lead to convincing plausible stories about how that system behaves. And that philosophy might be useful for e.g. making decisions in the face of an uncertain future. But regardless of how logical it is, it does not produce scientific knowledge about the world around us. At best it produces rational results, not scientific ones.
In a sense, it's true that the descriptions above form a specific philosophy of science, but they're also empirically tested methodologies. They're the methodologies that have been used in the past to derive accurate representations of how the world around us works at a fundamental physical level. It is possible that economists (including Christiano et al) have come up with another path to knowledge about the world around us where you can make invalid but prima facie sensible assumptions about how things work and derive conclusions, but it isn't a scientific one.
Footnotes:
[1] Actually, the problem seems misidentified in a similar way that Friedman's "as if" methodology is misidentified: the idea is fine (in science it is called "effective theory"), but the application is flawed. Friedman seemed to first say matching the data is what matters (yes!), but then didn't seem to care when preferred theories didn't match data (gah!).

Interesting. I learned something!
ReplyDelete