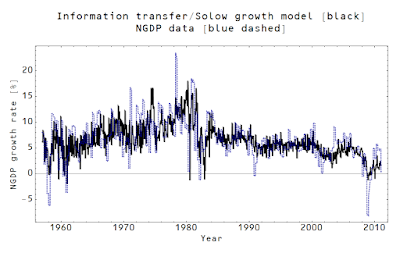
 |
| Show me the data! |
Ok, this is the last post on mathiness -- there's real work to be done!
I'd like to start off by saying I'm overall sympathetic to the complaints Paul Romer is making about his field. I agree! Certain economists seem to obfuscate their political assumptions with a blizzard of math [0]. Overall, he seems like a good guy ... and was essentially a physics major, which is a plus in my book!
The style that I am calling mathiness lets academic politics masquerade as science. Like mathematical theory, mathiness uses a mixture of words and symbols, but instead of making tight links, it leaves ample room for slippage between statements in natural versus formal language and between statements with theoretical as opposed to empirical content.
I cheered. There was no mention of Solow in Romer's blog post -- I even thought he might be after the neoclassical embrace of the model as evidenced by Marginal Revolution University's whole unit on it (a unit filled with obfuscated political assumptions).
[mathiness] leaves ample room for slippage ... between statements with theoretical as opposed to empirical content.
Romer seems to be more upset about the lack of "tight links" -- essentially the lack of formal rigor. The key issue I have is that Romer believes this:
We assume that the measure of a country’s production locations is proportional to its population, since locations correspond to markets and some measure of people defines a market.
McGrattan and Prescott (2009)is somehow less problematic than this [1]:
Output is to be understood as net output after making good the depreciation of capital. About production all we will say at the moment is that it shows constant returns to scale. Hence the production function is homogeneous of first degree. This amounts to assuming that there is no scarce nonaugmentable resource like land. Constant returns to scale seems the natural assumption to make in a theory of growth.
Solow (1956)
Constant returns to scale are not assumed because they are empirically observed. Solow essentially says he assumes constant returns to scale because it seems to be the just the sort of assumption one makes when defining a theory of growth. (Wait ... did you just say there is no such thing as land?) Why not just say you're assuming constant returns to scale because it makes the math easier and narrows down the possibilities of the production function?
But the worst part of this is that it doesn't even make sense in terms of the economics of growth. I double my factories and my labor force, I double my output? Here is a short list of possible effects that would fight in different directions, but generally away from constant returns to scale:
- Additional factories mean that the managerial and labor force could be less skilled on average (limited resource, decreasing returns to scale) [2]
- Additional factories allow for more eyes and more possibilities to find tweaks that improve production (increasing returns to scale)
- Additional capital and labor mean better paying jobs that incentivize the creation of amenities and higher standards of living (increasing returns to scale)
- Additional captial and labor mean develop more experience, expanding the the source of new ideas and businesses (increasing returns to scale)
However, the assumption of constant returns to scale puts all of these effects into a new piece that gets the name Total Factor Productivity (TFP) ... that becomes a mysterious factor responsible for most of economic growth. If you look at it empirically, the Cobb-Douglas production function works just great if you just drop the extra theoretical assumptions.
I'm not saying economists don't know about these things -- Romer is one of the foremost experts on growth economics. I am saying theoretical models and assumptions are trumping empirical analysis. Theoretical assumptions create empirical problems that must be solved with additional assumptions (auxiliary hypotheses) -- a regressive research program.
Prescott and Lucas aren't Romer's problem. Romer's problem has been around for a lot longer than their recent papers (at least 1956, but really well before then). Connection with empirical data is the purgative growth economics needs. It is the purgative macroeconomics needs. Empirics aren't going to bow down to mathiness regardless of whether it is a lack of rigor or political theoretical assumptions.
...
PS Romer's mathiness doesn't just exist in economics -- it exists in theoretical particle physics and string theory. And the reason is similar: a lack of experimental data. There's no real politics in string theory, but that doesn't stop what are essentially alliances from forming around the big figures in the field. The way you get ahead is no longer solving empirical puzzles or predicting new experimental results. You get ahead by impressing a key figure in the field with your genius.
This is to say that it's not because economics has to deal with real world policy that politics dominates -- it's the lack of empirical data that lends itself to a system of alliances. And instead of forming a new type of alliance out of whole cloth, it takes one off the shelf (common everyday left-right politics). That politics is like the cosmic microwave background radiation -- the higher energy density areas lead to galaxies and the lower density to voids. "Saltwater" economics forms on the politically liberal coasts of the US, "Freshwater" in its more conservative interior.
No amount of discussion about methodology or mathiness will dislodge these alliances. Empirical data is the only thing that can. Noah Smith says macro data is uninformative. I call bullshit on that. Macro data can only be uninformative if your models are too complex for the data you have. Drop the complex models and show some simple models with lines going through data.
That's why I hope all of you out there reading these economics blogs start asking to see the data. Ask to see lines going through the data. If an econoblogger's model can't produce agreement with empirical data, don't be afraid to call it garbage. Tell that econoblogger they're away with the fairies. I get my stuff called garbage all the time; trust me it doesn't hurt my feelings (but then I like arguments). It's even helpful sometimes! And at least I disclose the models and show how they do with empirical data.
[0] In a sense, that is something that is refreshing about the right-leaning economist/blogger Scott Sumner. Sumner seems to be saying there is no mathematical theory -- it's all political belief.
[1] Paul Romer: "The Solow model is an example of excellent theory."
[2] We all see this first hand when a restaurant we like opens another location that is never quite as good as the original. It's also the trend towards mediocrity that comes with ubiquity e.g. Wolfgang Puck canned soups.
This:
ReplyDeletehttp://econospeak.blogspot.com/2015/05/mathiness-and-growthiness.html
Expresses some of the same sentiments I do here ... with a better title.
Hi Jason,
ReplyDeleteWhen you wrote "is somehow less problematic than this" did you mean 'is somehow more problematic than this' or am I just confused... ?
Hi John,
DeleteThe clearest way to say it is that Romer thinks:
Solow > Prescott
Whereas I think
Solow ≈ Prescott
So Romer thinks the quote I show is less problematic than the Solow quote.
Romer's reason for calling out the idea that production locations are proportional to population is that in perfect competition (as opposed to the monopolistic competition Romer favors) there are an infinite number of firms. It is true that it is nonsensical to say that production locations are proportional to an infinite quantity. But that sloppy language is easily fixed by shifting to densities -- production location density is proportional to population density, or by saying perfect competition isn't among an infinite number of firms (which is nonsense on the face of it) but among N firms where N >> 1 -- you are effectively ignoring terms that are o(1/N), which would include e.g. fluctuations around means and so forth.
Assuming a large number of firms and production location density proportional to population density aren't that weird of simplifying assumptions -- and definitely not weirder than assuming constant returns to scale without any real explanation.
Excellent as usual, Jason! Sure, looking at data in economics is about as messy as it gets, but without it you are really nowhere. My (limited) understanding is that back in the 1980s there was some real hope that string theory could eventually provide a parsimonious theory of force unification, but as more was learned about the math things really got bogged down without any obvious way to distinguish amongst the multiplicity of different solutions, given you couldn't match with experimental results.
ReplyDeleteThanks, Todd.
DeleteIt was always known that matching data with experiment was going to be basically impossible. The string scale is the Planck scale and is 10^19 GeV, requiring an accelerator ~ 10^16 times as powerful as CERN.
However, I think one major success of string theory (it is a theoretical success) is calculating black hole entropy:
http://arxiv.org/abs/hep-th/9601029
There still is the string theory landscape (that multiplicity of solutions), but maybe maximum entropy is a guide there ...
http://arxiv.org/abs/1203.0307
The problem with lines going through data is that the curves are altered to fit the belief.
ReplyDeleteWe live in a Procrustean world, where 40 years of policies trying to fit the world into a pretty theory have crippled the data. We have no idea what the 7ft or 4ft entity could do because they have all had their feet chopped off, or been subjected to the rack.
Hi Neil,
DeleteI'm staying optimistic that things can get better! It's true that a lot of economics was developed because it gave comfort to the comfortable ... maybe we can make this story the new narrative. John Quiggin is doing some good work:
http://crookedtimber.org/2015/05/19/the-most-misleading-definition-in-economics-draft-excerpt-from-economics-in-two-lessons/