A continuing exchange with UnlearningEcon prompted me to revisit an old post from two and a half years ago. You don't need to go back an re-read it because I am basically going to repeat it with updated examples; hopefully my writing and explanation skills have improved since then.
The question UnlearningEcon asked was what good are fits to the (economic) data that don't come from underlying explanatory (behavior) models?
The primary usefulness is that fits to various functional forms (ansatze) bound the relevant complexity of the underlying explanatory model. It is true that the underlying model may be truly be incredibly complex, but if the macro-scale result is just log-linear (Y = a log X + b) in a single variable then the relevant complexity of your underlying model is about two degrees of freedom (a, b). This is the idea behind "information criteria" like the AIC: more parameters represent a loss of information.
My old post looks at an example of thermodynamics. Let's say at constant temperature we find empirically that pressure and volume have the relationship p ~ 1/V (the ideal gas law). Since we are able to reliably reproduce this macroscopic behavior through the control of a small number of macroscopic degrees of freedom even though we have absolutely no control over the microstates, the microstates must be largely irrelevant.
And it is true: the quarks and gluon microstate configurations (over which we have no control) inside the nucleus of each atom in every molecule in the gas are incredibly complicated (and not even completely understood ‒ it was the subject of my Phd thesis). But those microstates are irrelevant to understanding an ideal gas. The same applies to nearly all of the information about the molecules. Even vibrational states of carbon dioxide are irrelevant at certain temperatures (we say those degrees of freedom are frozen out).
The information equilibrium framework represents a way to reduce the relevant complexity of the underlying explanatory model even further. It improves the usefulness of fitting to data by reducing the potential space of the functional forms (ansatze) used to fit the data. As Fielitz and Borchardt put it in the abstract of their paper: Information theory provides shortcuts which allow one to deal with complex systems. In a sense, the DSGE framework does the same thing in macroeconomics. However, models with far less complexity do much better at forecasting ‒ therefore the complexity of DSGE models is probably largely irrelevant.
A really nice example of an information equilibrium model really bounding the complexity of the underlying explanatory model is the recent series I did looking at unemployment. I was able to explain most of the unemployment variation across several countries (US and EU shown) in terms of a (constant) information equilibrium state (dynamic equilibrium) and shocks:
Any agent based model that proposes to be the underlying explanatory model can't have much more relevant complexity than a single parameter for the dynamic equilibrium (the IT index restricted by information equilibrium) and three parameters (onset, width, magnitude) for each shock (a Gaussian shock ansatz). Because we can reliably reproduce the fluctuations in unemployment for several countries with no control over the microstates (people and firms), then those microstates are largely irrelevant. If you want to explain unemployment during the "Great Recession", anything more than four parameters is going to "integrate out" (e.g. be replaced with an average). A thirty parameter model of the income distribution is going to result in at best a single parameter in the final explanation of unemployment during the Great Recession.
This is not to say coming up with that thirty parameter model is bad (it might be useful in understanding the effect of the Great Recession on income inequality). It potentially represents a step towards additional understanding. Lattice QCD calculations of nuclear states is not a bad thing to do. It represents additional understanding. It is just not relevant to the ideal gas law.
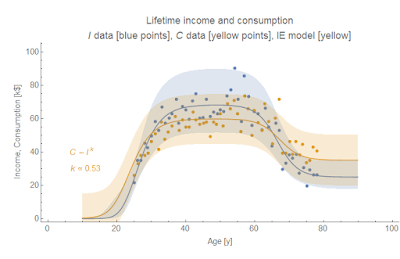
Another example is my recent post on income and consumption. There I showed that a single parameter (the IT index k, again restricted by information equilibrium) can explain the relationship between lifetime income and consumption as well as shocks to income and consumption:
Much like how I used an ansatz for the shocks in the unemployment model, I also used an ansatz for the lifetime income model (a simple three state model with Gaussian transitions):
This description of the data bounds the relevant complexity of any behavioral model you want to use to explain the consumption response to shocks to income or lifetime income and consumption (e.g. short term thinking in the former [pdf], or expectations-based loss aversion in the latter [pdf]).
That adjective "relevant" is important here. We all know that humans are complicated. We all know that financial transactions and the monetary system are complicated. However, how much of that complexity is relevant? One of the issues I have with a lot of mainstream and heterodox economics (that I discuss at length in this post and several posts linked there) is that the level of relevant complexity is simply asserted. You need to understand the data in order to know the level of relevant complexity. Curve fitting is the first step towards understanding relevant complexity. And that is the purpose of the information equilibrium model, as I stated in the second post on this blog:
My plan is to produce an economic framework that captures at least a rich subset of the phenomena in a sufficiently rigorous way that it could be used to eliminate alternatives.
Alternatives there includes different models, but also different relevant complexities.
The thing that I believe UnlearningEcon (as well as many others that disparage "curve fitting") miss is that curve fitting is a major step between macro observations and developing the micro theory. A good example is blackbody radiation (Planck's law) in physics [1]. This is basically the description of the color of objects as they heat up (black, red hot, white hot, blue ... like stars). Before Planck derived the shape of the blackbody spectrum, several curves had been used fit the data. Some had been derived from various assumptions about e.g. the motions of atoms. These models had varying degrees of complexity. The general shape was basically understood, so the relevant complexity of the underlying model was basically bounded to a few parameters. Planck managed to come up with a one-parameter model of the energy of a photon (E = h ν), but the consequence was that photon energy is quantized. A simple curve fitting exercise lead to the development of quantum mechanics! However, Planck probably would not have been able to come up with the correct micro theory (of light quanta) had others (Stewart, Kirchhoff, Wien, Rayleigh, Rubens) not been coming up with functional forms and fitting them to data.
Curve fitting is an important step, and I think it gets overlooked in economics because we humans immediately think we're important (see footnote [1]). We jump to reasoning using human agents. This approach hasn't produced a lot of empirical success in macroeconomics. In fact ‒ also about two and a half years ago ‒ I wrote a post questioning that approach. Are human agents relevant complexity? We don't know the answer yet. Until we understand the data with the simplest possible models, we don't really have any handle on what relevant complexity is.
...
Footnotes
[1] I think that physics was lucky relative to economics in its search for better and better understanding in more than one way. I've talked about one way extensively before (our intuitions about the physical universe evolved in that physical universe, but we did not evolve to understand e.g. interest rates). More relevant to the discussion here is that physics, chemistry, and biology were also lucky in the sense that we could not see the underlying degrees of freedom of the system (particles, atoms, and cells, respectively) while the main organizing theories were being developed. Planck couldn't see the photons, so he didn't have strong preconceived notions about them. Economics may be suffering from "can't see the forest for the trees" syndrome. The degrees of freedom of economic systems are readily visible (humans) and we evolved to have a lot of preconceptions about them. As such, many people think that macroeconomic systems must exhibit the similar levels of complexity or need to be built up from complex agents ‒ or worse, effects need to be expressed in terms of a human-centric story. Our knowledge of humans on a human scale forms a prior that biases against simple explanations. However, there is also the problem that there is insufficient data to support complex explanations (macro data is uninformative for complex models, aka the identification problem). This puts economics as a science in a terrible position. Add to that the fact that money is more important to people's lives than quantum mechanics and you have a toxic soup that makes me surprised there is any progress.




The main question I have is this: do the expressions you've obtained by curve fitting make good out-of-sample predictions?
ReplyDeleteThat's been my general project here and the answer has been yes. In fact, the unemployment rate model above ended up being tested out of sample by accident (FRED doesn't have the most up to date data). And this ongoing test is doing very well, even accounting for the US election.
DeleteMore out-of-sample forecasts are here.
I would like to say that info eq goes beyond just curve fitting and does something you could call "theory fitting" -- a lot of standard econ can be represented in terms of info eq. What I find especially interesting is that some of the standard econ requires info eq relationships that are rejected empirically (notably, the simple three-equation New Keynesian DSGE model).
"Because we can reliably reproduce the fluctuations in unemployment for several countries with no control over the microstates (people and firms), then those microstates are largely irrelevant"
ReplyDeleteReproduce, in what sense? Create a model with comparable dynamics?
There are things that aren't reproducible, even experimentally. Often, these are EXACTLY the things that social critics and historians need to be concerned with.
Models and experiments can't tell us many things.
It is my experience working with computer programs, that until you get your mental conceptual model EXACTLY right, you are just going to be completely lost trying to debug problems.
Even with the best mathematical tools and best experimental methods, you are limited by certain things.
I guess this is why I have been less inclined to pursue the mathematical angle to exploring econ(i was an undergrad Math/CS major), and more inclined to view econ through a philosophical lense.
You are limited by the cultural practices for creating numerical representations of social outcomes.
I might be more interested in seeing examples of your mathematical tools applied to the animal kingdom. I think humans do a better job of describing the animal kingdom objectively. I would love to see information theory mathematical tools applied to bird migration or behavior in ant colonies, as examples.
Perhaps I'm misunderstanding the big picture of what you're doing. I am usually excited by the prospect of mathematical tools telling us things about ourselves that we can't see otherwise. But I think you may have bought into some of the traditional perspectives assumed by the econ profession a little too much.
I wish I knew information theory well enough to discuss and explore your work in detail. I've only seen a little bit of coding theory and stuff like hamming distance. I guess I've favored computational theory, with its mappings, reductions, and complexity classes, more than info theory.
Other than that, it looks like very fascinating stuff to create information theory descriptions of these important economic ideas.
I don't think traditional economic concepts are useless, I just think the way they are applied often involves invalid assumptions, and fails to recognize the true complexity of our social and cultural systems.
By reproducible, I mean the description of the unemployment rate or income/consumption is reproducible across different countries or under different conditions. I wrote a post a couple years ago about how the recovery from high unemployment seems about the same over the entire post-war period. The description of that data is reproducible, and it's reproducible regardless of (as I said at the link) "the internet, inequality, jobless recoveries, war, government spending, unemployment benefits, ... technology, ... etc". That's what I mean by not controlling the microstates and getting a reproducible result.
DeleteRegarding your statement that traditional economics "fails to recognize the true complexity of our social and cultural systems", what do you mean by complexity? I wrote an entire post on this subject. As a physicist, I'm well versed in complex systems and the economy may be a complicated system, but there is no evidence that it is a complex system -- unless by complex you just mean complicated. In fact, there probably never will be enough data to distinguish a complex system from a linear system subjected to stochastic shocks (see here).
But does recognizing the true complexity give us a better empirical description? Then there's no reason to say "recognize the complexity"; just show us the better empirical description and we'll be forced to deal with the complexity.
However, the unemployment rate above shows that complicated human behavior and government interventions are only a small perturbation to the underlying dynamics.
It was a mistake to use the word complexity there. But let's focus on the important issue.
ReplyDeleteKnowledge does not exist without reproducibility, and certainly, scientific processes have no applicability without reproducibility.
I appreciate that complexity can be a way of mathematically characterizing the behavior of systems. I also appreciate that the emergent systemic behavior of a collection of complex agents can still lead to simple behavior at the systems level.
Employment and unemployment can't be defined consistently across anthropological contexts. It is much easier to define biological variables like mortality, population growth, etc. The social variables depend on social ideas created within the social system, instead of scientific/mathematical ideas applied to the system by observers and researchers.
Within specific contexts, these biological and social variables can correlate in robust ways. In the modern world, people with better employment or income enjoy better health. But if you change social narratives or political structures, it's possible for those changes to invalidate any empirical observations. Though you seem to be arguing that this tends not to happen.
There may be a wide variety of systemic configurations which behave in similar ways. Consider elementary cellular automata: http://mathworld.wolfram.com/ElementaryCellularAutomaton.html
The fractal structure of serpenski's triangle appears many times, with some variation. Many rules have relatively trivial behavior. But a few rules have behavior that exhibits genuine complexity. Rule 110 has been demonstrated to be Turing complete.
As a computer programmer, I have a strong bias. I conduct empirical tests for the purpose of debugging applications with the goal of creating systems that achieve specific goals, using programs.
There is a huge space of broken programs and disfunctional systems.
Programmers have to be very selective in the process of isolating variables for debugging problems. We can't afford to try everything methodically. It's easy to be superstitious or rely on serendipity to try to fix a broken program. Experience trains us to be both selective and methodical, in debugging programs, if it's possible to be both. Experience trains us to recognize assumptions and prioritize the tests we conduct accordingly.
Our political programs have specific goals. Why can't they achieve these goals? That is my concern. A trillion systems where there is an unavoidable tradeoff between inflation and unemployment are irrelevant to me.
I only care about the political structures and relationships that can facilitate both full employment and monetary stability, for example. I believe there are specific social issues to be debugged to achieve these goals.
I hope that gives a better picture of the way I think about economic problems. If I failed to communicate effectively in my comment, I hope this clarifies some things.
"Employment and unemployment can't be defined consistently across anthropological contexts."
DeleteThis is a bit of strict requirement, no? "Writing" also can't be consistently defined across anthropological contexts (I'm not talking about different languages, but the fact that some cultures didn't have writing); that does not make it an invalid thing to understand e.g. its information carrying capacity (one to two bits per letter in English).
If unemployment data didn't have any recognizable structure, then the argument that unemployment is hard to define across cultures might carry more weight. But it appears to have some structure, so there must exist a way to define it in a meaningful way regardless of whether that definition applies to all manifestations of human societies.
"A trillion systems where there is an unavoidable tradeoff between inflation and unemployment are irrelevant to me."
This is where I appeal to the division of labor. Some of us work on some things, others work on others. So it's fine by me if you want to work on the problem of achieving goals through politics. I will continue to work on looking for mathematical regularities in economic data.
"I only care about the political structures and relationships that can facilitate both full employment and monetary stability ..."
Depending on your definition of monetary stability, this may not be possible. I showed with one model that is fairly empirically successful that fixed interest rates and fixed inflation are not possible.
It may be that monetary stability and full employment are theoretically incompatible. The former seems to be an impossibility on its own if money carries information. However that far from settles the question. What political structures can facilitate what goals depends largely on whether those goals are well-defined or achievable (not saying they aren't).
One's political goal may be to build a faster-than-light ship to colonize other planets. That violates the laws of physics as we currently understand them, therefore no political structure is going to facilitate it. Inflation seems to be fundamental aspect of the information theory prices of different baskets of goods. But maybe it's directly related to the labor force, in which case moving towards not just a low unemployment rate, but high labor force participation will always be accompanied by massive inflation.
...
There is a tendency among everyone (economists or not) to think about the "big ideas" and the politically relevant issues in economics before diving into the messy details. The current paradigm is amenable to that: human agents and their thoughts are the substrate on which economic theory is built. If economics is just human decisions, then politics can affect those decisions.
However if economics is at its heart more about information and the mathematical structure of opportunity sets, then politics may have no effect and you may just have to mitigate the bad aspects of it.