Modeling macroeconomic fluctuations

Since I've been heavy into the policy implications of the information transfer model in the past few posts, I thought I'd return to some more speculative research. I've touched on the topic of macroeconomic fluctuations before (see e.g. [1], [2]), but I thought I'd do some thinking out loud.

The main idea is that the information transfer model P:D→S with where demand information (ID) is equal to supply information (IS) represents an upper bound P on the price P in the market**. Since information transferred to the supply can never be greater than the information coming from the demand, the actual price realized P* in the market is going to fall below this level (or the supply or demand will fluctuate). If ID > IS for aggregate demand D and aggregate supply S, then let's define 0 < ε < 1 such that ε ID = IS where we will call ε  the information transfer efficiency. Our model of macroeconomic fluctuations is then a model of fluctuations in ε where the efficiency in each individual market {ε1, ε2, ε3 ...} are all proportional to ε. This model will turn out to be at best a first order approximation but interesting nonetheless. Yes, this can be considered just a re-hash of total factor productivity, but I think macroeconomic fluctuations arising from information transfer inefficiency in the market rather than animal spirits or that the cycle represents a real thing is a useful re-framing of the conversation.

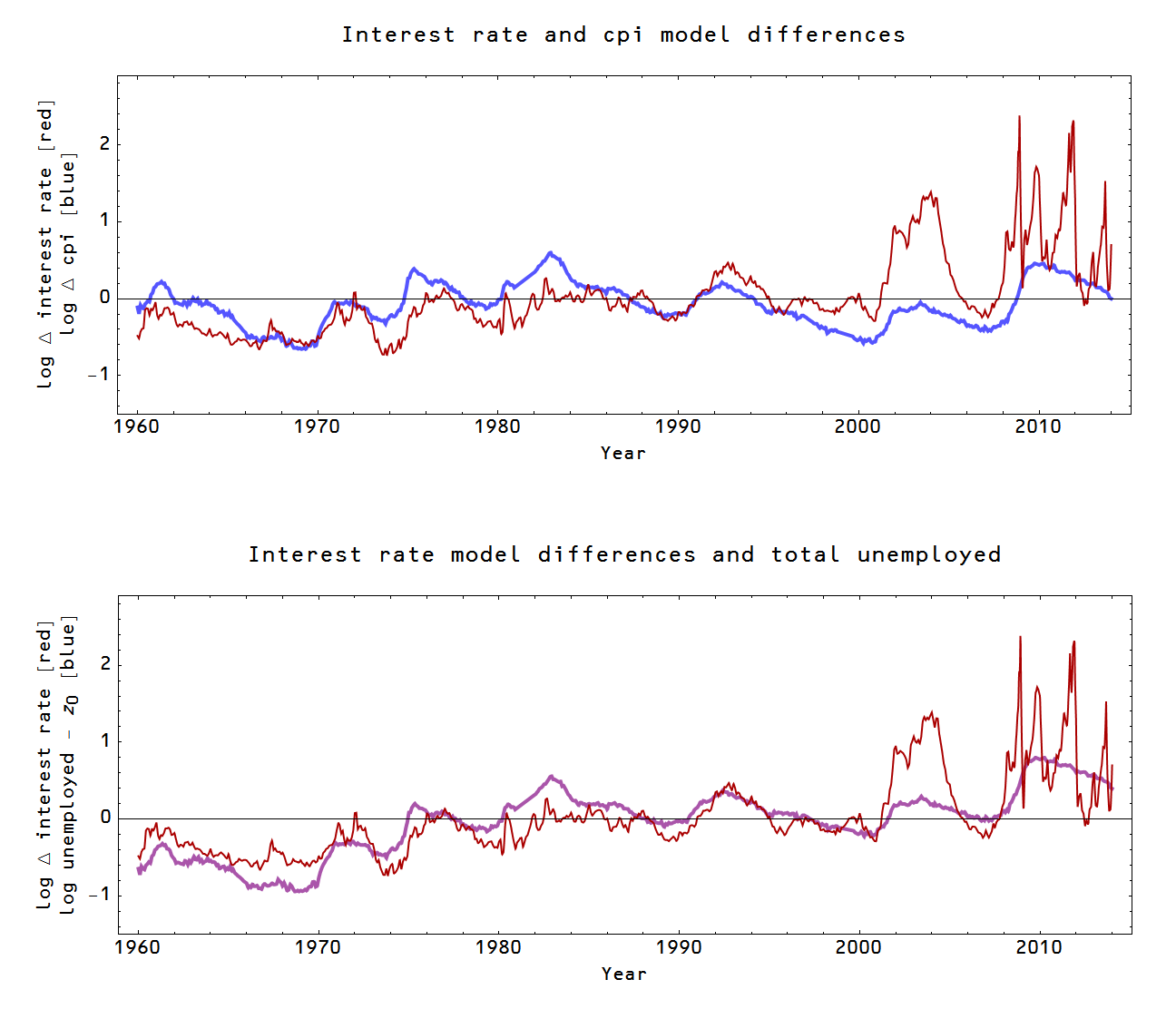
To be concrete, we'll look at two markets: r:NGDP→MB (interest rate) and P:NGDP→U (unemployment). P will be described by the CPI less food, energy, U is the total number of people unemployed and r is the 3-month and 10-year interest rate (using the monetary base MB =  reserves + currency for the former and just the currency component for the latter -- see here). Here are the model fits and the data:

In the interest rate market, the price (interest rate, especially the 3-month rate) appears to do the lion's share of the adjusting to changes in information transfer efficiency ε while in the employment market, the number of people becoming unemployed does the adjusting. This makes intuitive sense: there is an active market for US treasuries while NGDP and the base don't move very fast. Likewise in the unemployment market, NGDP and the price level are slower to adjust, so layoffs do the adjusting. In the picture above, I've drawn a red arrow to suggest the possibility that these fluctuations are related to the same underlying fluctuating information transfer efficiency ε per the thesis of this post. The (log) differences (Δ) in the models -- in the case of the interest rate market it is the double difference (10 year rate model - data) - (3 month rate model - data) -- show qualitatively similar behavior (top graph):

In the bottom graph (purple), I have a simpler model log U - z0 instead of the CPI model differences which seems to work as well if not better. Both the simpler unemployment model and the CPI unemployment model miss the big fluctuation in the interest rate market in the mid 2000s and I believe we are seeing zero-bound related effects in the interest rate market post-2008. 

These results imply that the information transfer efficiency model (ε-model) is a good order of magnitude estimate, but still not ready for prime time. There appears to be a significant fluctuating component unique to each individual market.

** ID = IS. The shorthand notation P:D→S means that the price P is detecting information transferred from the demand (information source) to the supply (information destination). See here.

UPDATE: Edited for a marginal improvement in clarity in red and cross-outs.