Dan Davies had this analogy on twitter for macro without a financial sector:
@dsquareddigest: @Frances_Coppola @ericlonners it's as if there was an epidemic of hepatitis and half the doctors had to look up what the liver was for.
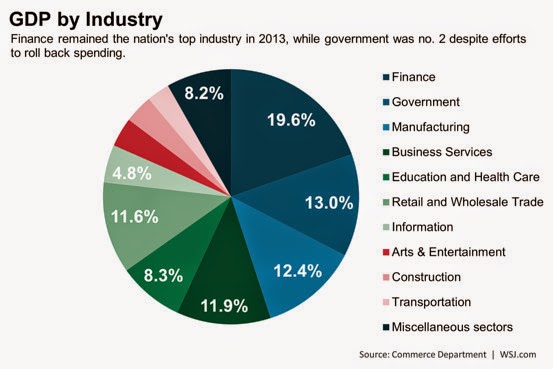
And if we look at e.g. the data presented in this blog post, we can see that the financial sector is indeed a sizable chunk of NGDP at 19.6% in 2013.
Let's try to build a picture of what such a "financialized" economy looks like starting from the maximum entropy view of the information equilibrium model. Borrowing pictures from that post, a snapshot of an ordinary economy looks something like this:
Each box represents a business or industry, and at any time they might find themselves on the decline or growing, with most growing near the average rate of economic growth for the whole economy.
As we can see in the pie chart, though, there should be at least one very large box that moves in concert: the government. Generally, due to coordination by the legislative branch, government spending can move as a single unit -- e.g. across the board spending or tax cuts.
Now inside a single industry, the individual units won't necessarily be coordinated -- in fact, e.g. Ford and GM might be anti-correlated with one surging in profits while the other loses market share. Domestic manufacturing in general can rise or decline (crowded out by imports), but overall the result will be a lot less coordinated than government spending (except e.g. in a recession when all growth slows).
But what if the other big slice in the pie chart is coordinated? The financial sector could be as coordinated as government spending with markets effectively acting as the legislative branch. If we put government and the financial sector (to scale) in our snapshot, we get something that looks like this:
I've put government (in blue) growing at roughly the modal rate and the financial sector (in gray) outperforming it.
Now I've already looked at what happens when the government sector moves around; what we're concerned with today is the financial sector. If the financial sector is coordinated (through market exchanges or inter-dependencies), a big financial crisis can make the entire sector enter a low growth (or declining) state like this:
This is a far more serious loss of entropy than an uncoordinated sector of the same size with 50% (coordinated fraction = 0.5) of the states going from growth states to declining states, pictured here:
A calculation using the Kullback-Liebler divergence has the former version resulting in a loss of entropy of 4%, while the latter loses only 1%. In general, it looks like this:
One way to visualize the uncoordinated case is the dot-com bust where there were many different actors in the sector as opposed to the relatively smaller number of financial companies (q.v. "contagion") in the highly coordinated case.
Simply because it represents a large fraction of the US economy and is highly coordinated by exchanges (a significant bad day on the S&P500 is usually a significant bad day on other exchanges -- even around the world), it is plausible to posit the financial sector can move as a single unit, much like the government sector (coordinated instead by political parties).
We can think of the financial sector F as analogous of a second "government" sector and write:
(This is a heuristic designation -- F would specifically be carved out of C, I, G and NX as appropriate, and the exact definition would take some econometrics work.)
Financial crises would be much like government austerity, except they would be by definition procyclical -- being more likely when a recession happens, being the cause of a recession [1], or even being synonymous with a recession. A surging market is not very different from a surge in government spending; a collapsing market is not very different from a fall in government spending. That is to say a good model of the financial sector would simply be to dust off those old models of the government sector.
[1] I still think of recessions as avalanche events, but the financial sector can be the large rock that precipitates the cascade.





The arguments about including the financial sector in macro models are not so much about the financial sector’s own contribution to GDP. Rather, they are about the financial sector’s contribution to the money supply.
ReplyDeleteA cartoon version of the mainstream’s view of money is that money is created by the central bank and that commercial banks merely act as an intermediary between savers and borrowers. At the macro level, it doesn’t matter who is spending the money so banks don’t matter.
A cartoon version of the alternative ‘endogenous money’ view is that commercial banks create money when they make loans, and borrowers destroy money when they repay those loans, so banks and lending do matter. The endogenous money people use the term ‘loanable funds’ to describe the mainstream view.
This is at the very heart of macro. The mainstream appears to think that central banks push money into the economy. Endogenous money says that demand for goods and services in the economy pulls money out of the banking system. We discussed this briefly previously when I used the analogy of whether a car will be driven further because it has more fuel (like money push) or whether the driver’s desire to drive the car further will cause more fuel to be used (like money pull).
I agree with your comment about recessions being like avalanches. Banks can create avalanches in other sectors by forcing debtor businesses into bankruptcy. This then removes those businesses’ contributions to GDP. That then impacts on the customers and suppliers of the removed businesses e.g. a supplier will not get paid for recent business and will not get future business. This can cause an avalanche effect. Also, banks borrow from other banks so, if one bank gets into trouble, it can also threaten an avalanche within the banking system. Also, if a bank failure were to cause business or household savings to be lost, that could cause a further avalanche and general panic in the wider economy. (We have deposit insurance to prevent / contain this type of panic).
The Bank of England published a couple of papers last year which supported the endogenous money perspective.
http://www.bankofengland.co.uk/publications/Documents/quarterlybulletin/2014/qb14q1prereleasemoneyintro.pdf
http://www.bankofengland.co.uk/publications/Documents/quarterlybulletin/2014/qb14q1prereleasemoneycreation.pdf
There are endless discussions between economists on this as it is one of the main dividing lines between New Keynesians and Post Keynesians. Here is a random example from Steve Keen.
https://www.creditwritedowns.com/2013/11/paul-krugman-nick-rowe-endogenous-money.html
Steve Keen also has a series of videos on this on his YouTube channel. Here is an example where he seems to be talking to a group of econophysicists. It includes a demo of his open source modelling software showing the difference between loanable funds and endogenous money.
https://www.youtube.com/watch?v=ICKD83sZ-qg
For some reason your comment got filtered; I fished it out.
DeleteI didn't call it out above, but in saying there is an F component that was analogous to the G in NGDP = C + I + F + G + NX was implicitly including things like 'Keynesian mutlipliers', so that the fall in GDP due to the direct contribution of F was increased due to multiplier effects (possibly the entropy loss calculated above is that multiplier).
Now the detailed effects behind the Keynesian multiplier -- regardless of whether it applies to F or G -- is something that the model I'm looking at is agnostic about. It could well be explained by endogenous money. However, with the limited number of observations of recessions (or the relatively limited time series in general) it is unlikely that detailed models could be unambiguously identified. That's the heart of this piece by Noah Smith:
http://noahpinionblog.blogspot.com/2013/04/the-reason-macroeconomics-doesnt-work.html
Alternative models don't give you alternate empirical data.
For example, in one of the BoE papers you cite above, they produce this graph (Chart A) of various measures of the 'money supply':
https://twitter.com/infotranecon/status/591660381858242560
Given the relative size of the fluctuations in the data and how closely they follow each other, there is not much you can do empirically to distinguish them. A model that uses notes and coin is not much different from M1 which is not much different from MZM; depending on the complexity of the model, it is unlikely you can rule out any of those choices. That is to say you can't differentiate empirically between a model that involves just the central bank (M0/notes and coins) and one that involves commercial banks (M1 or MZM).
That's one of the reasons I started working on the information equilibrium approach ... the model is so simplistic that there is enough empirical data to make a case for a particular version of the money supply.
That's not to say an endogenous money approach isn't the correct underlying model of the F-multiplier. I'm just saying there isn't enough data to distinguish the different detailed models of the F-multiplier.
Although the information equilibrium model also provides a mechanism (entropic forces) that doesn't need a detailed underlying model. Whether that explains all of the multiplier, or whether there are additional effects hasn't been determined.
In a sense, we have this model:
ΔNGDP ≈ (1 + e + x + y ...) ΔF
Where 1 is the direct impact of ΔF on NGDP, e is the entropic modification of the multiplier and x, y, ... etc are due to other impacts (like endogenous money or expectations or other effects).